Machine Learning for Magnetic Anomaly Navigation

Wright Brother Institute AI/ML Collider, 2023-05-17

Aaron Nielsen, Ph.D.

The views expressed in this article are those of the author and do not necessarily reflect the official policy or position of the United States Government, Department of Defense, United States Air Force or Air University.

Distribution A: Authorized for public release. Distribution is unlimited. Case No. 2023-0388.

Topics

• AFIT/ANT Center
  • Air Force Institute of Technology
  • Autonomy and Navigation Technology Center
• Magnetic Anomaly Navigation (MagNav)
  • Overview
• AI/ML Research Areas
  • Magnetic Anomaly Maps
  • Calibration and Compensation of Platforms

https://afit-eeng-magnav.github.io/2023-05-17-wbi-collider/

AFIT ANT Center

MagNav overview

Magnetic Anomaly Navigation Overview

Refrigerator magnet

Earth’s core field (compass)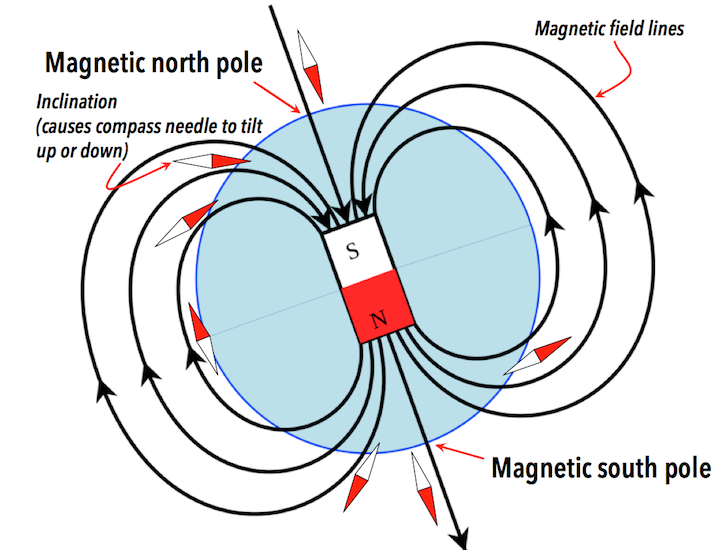

Crustal magnetic anomaly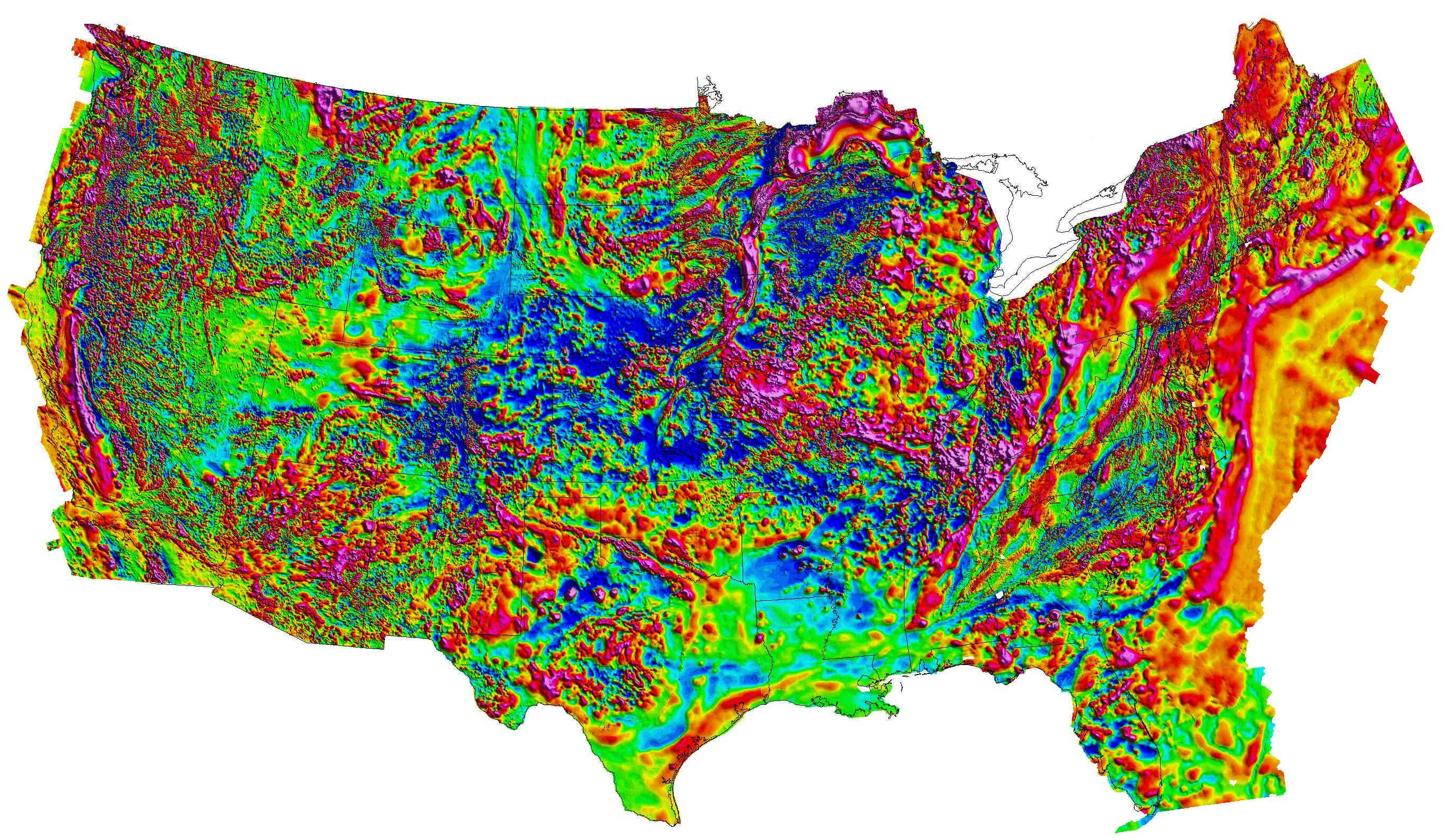

1 000 000 nT

50 000 nT https://www.ncei.noaa.gov/products/world-magnetic-model (Chulliat 2020)

Range \(\pm\) 500 nT
Resolution \(\sim\) 1 nT https://mrdata.usgs.gov/magnetic/ (Bankey et al. 2002)

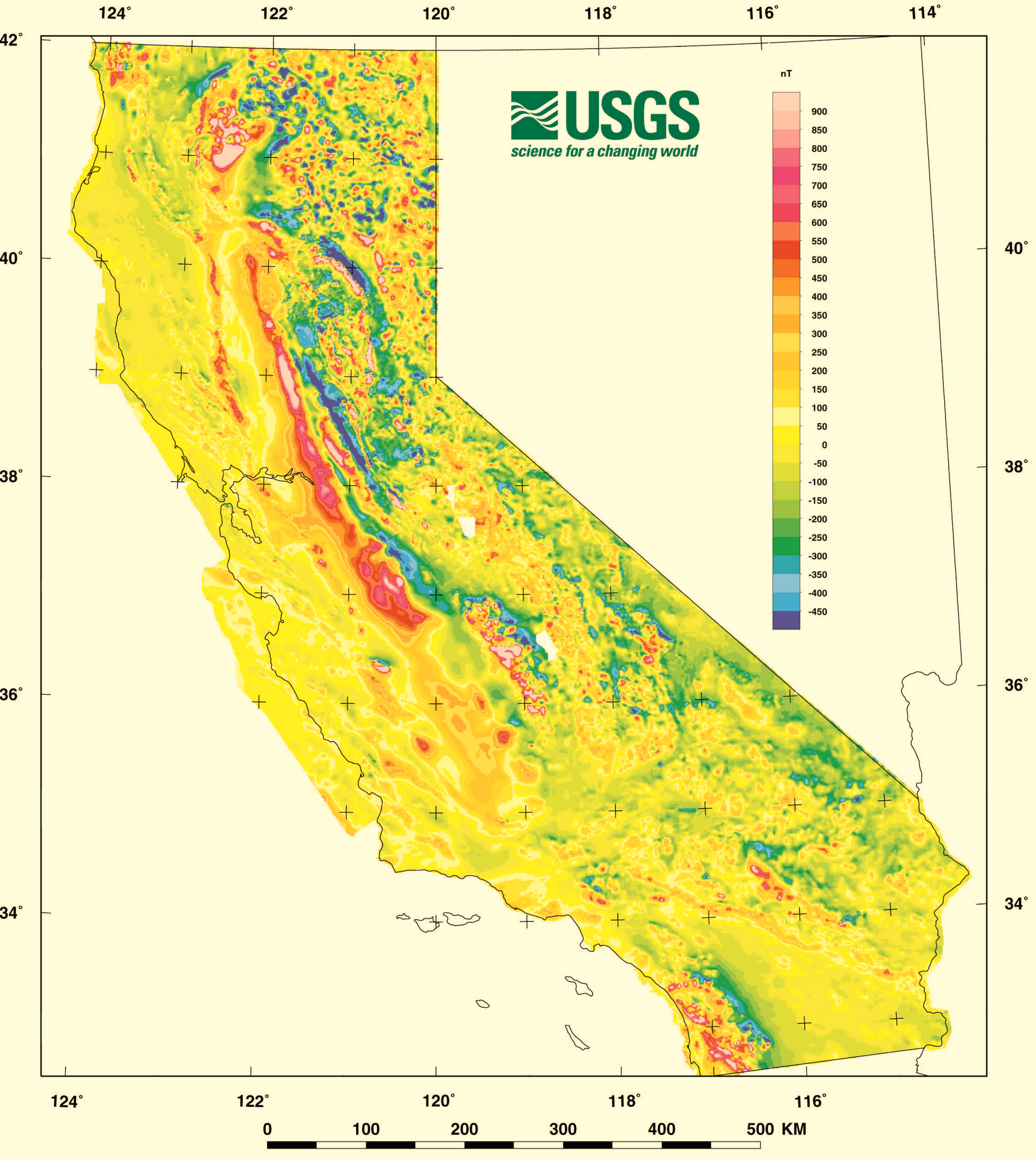
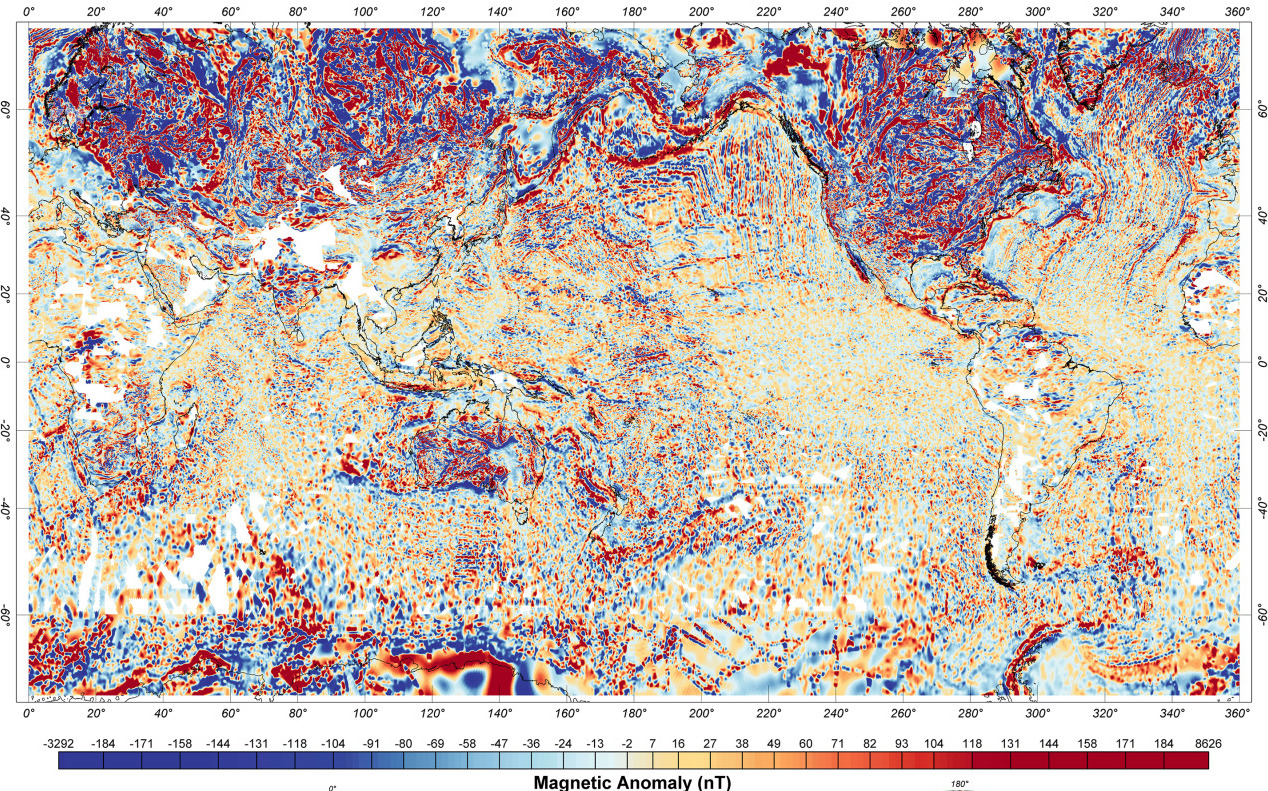
Map-based navigation

• Features are required to navigate
• Magnetic anomaly closely tied to geology
  • less variation in coastal region
  • direction variation in Central Valley
  • more structure in Sierra Nevada mountains
• Area and direction of travel make a difference
  (Roberts and Jachens 2000)

Earth Magnetic Anomaly Grid 2-arcsec v3

(Meyer, Chulliat, and Saltus 2017)

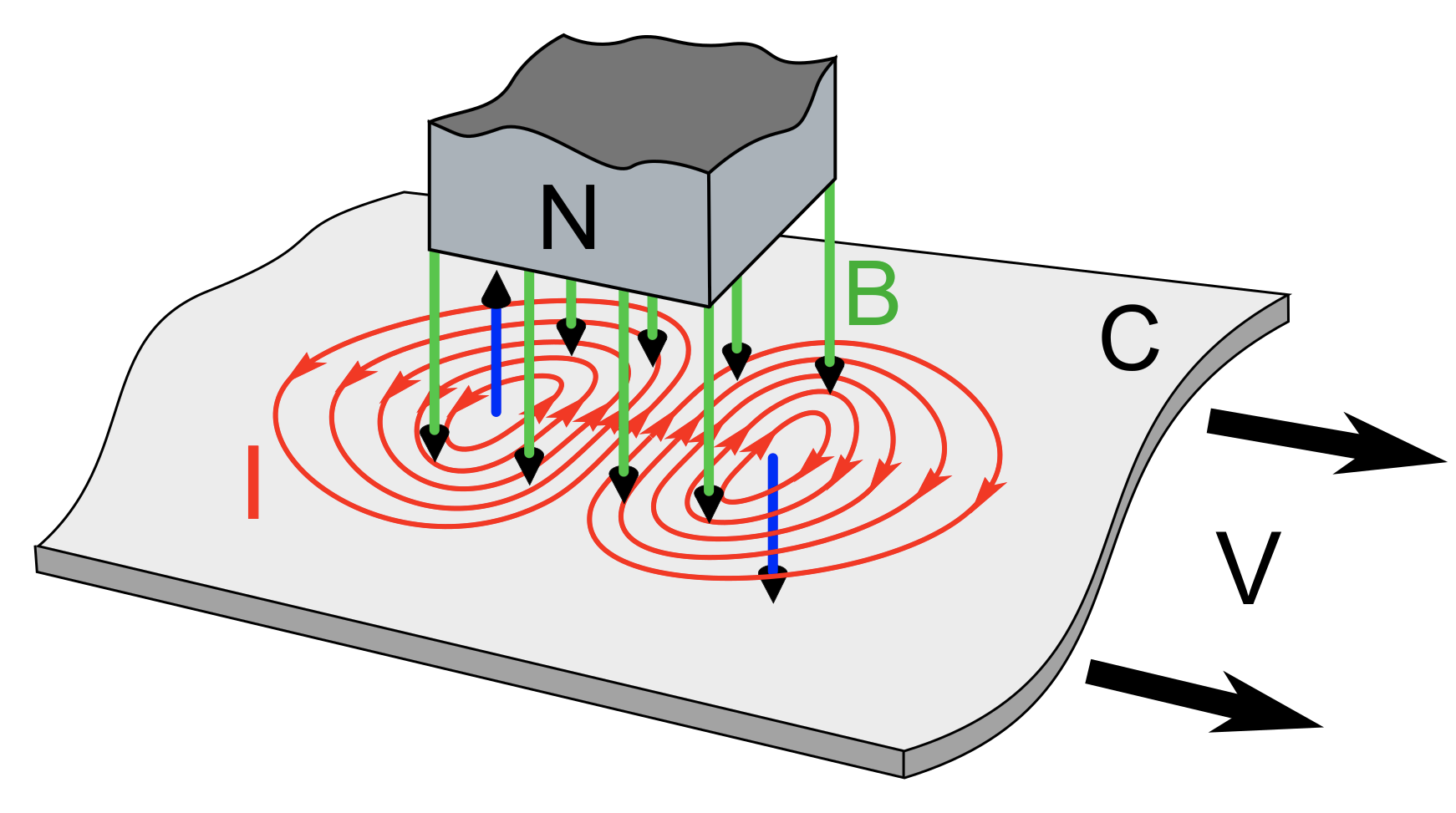
An airplane is a big magnet that flies

\(|\vec{B}| = |\vec{B}_\text{earth} + \vec{B}_\text{anomaly} + \vec{B}_\text{plane}|\)

Aircraft Calibration

Sensor placement and installation

• Engineered location
  • Stinger
• Survey for placement
• Non-magnetic fasteners

Degaussing

Algorithms

Sander Geophysics, Ltd

Published F-16 results

Approximately 60 meter position error

(Canciani 2021)

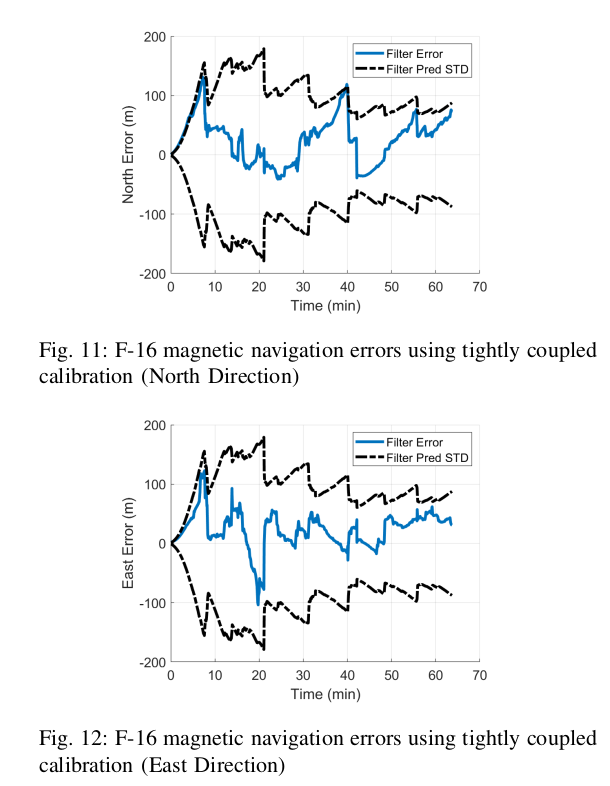
F-16 photos approved for public release by Edwards AFB Public Affairs Office. Public Release number 20438.

Standard calibration model - Tolles-Lawson

\[|\vec{B}| = |\vec{B}_\text{ext} + \vec{B}_\text{plane}|\]

\[ \begin{array}{ l B c B c B c } \vec{B}_\mathrm{Plane} & = & \vec{B}_\mathrm{Permanent} & + & \vec{B}_\mathrm{Induced} & + & \vec{B}_\mathrm{Eddy}\\ & = & \vec{P}_\mathrm{constant} {} & + &{} M_{3\times3} \vec{B }_\mathrm{Earth} {} & + & {} S_{3\times3} \frac{\partial}{\partial t} \vec{B}_\mathrm{Earth} \end{array} \]

\(M_{3\times3}\) is symmetric \(\rightarrow\) 6 independent elements

Total of 18 independent elements

Calibration manuevers - Tolles-Lawson

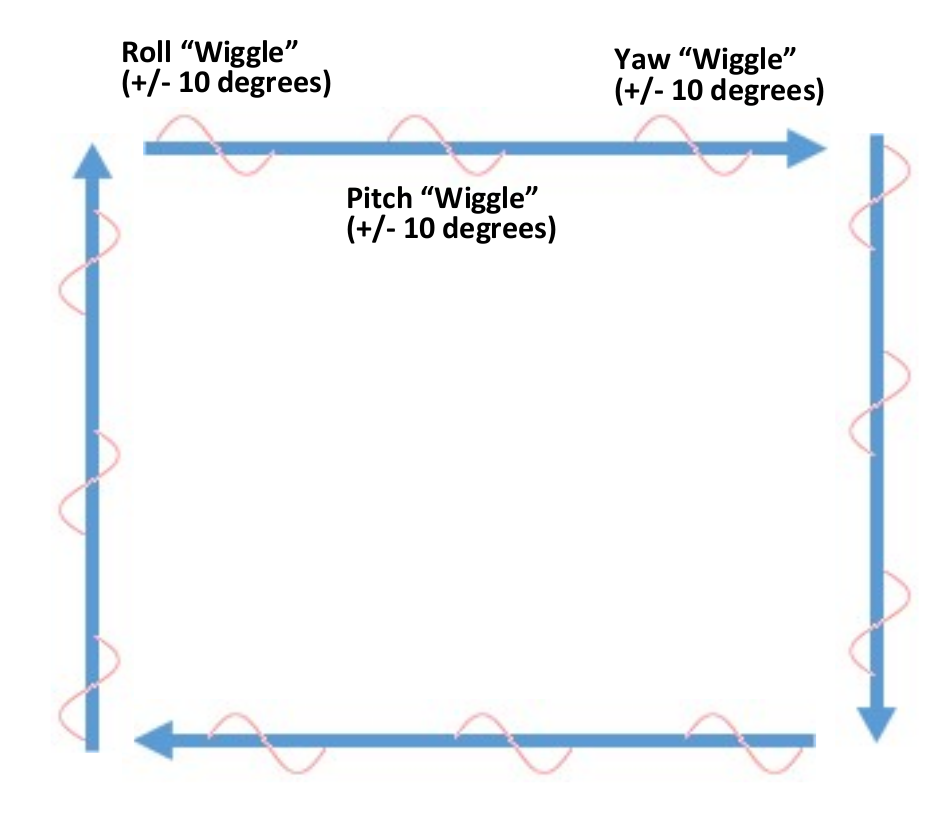
Fly the aircraft in a series of Roll, Pitch, Yaw maneuvers

• High-altitude

• Altitude of a known map

Maneuver angle should depend upon the expected aircraft dynamics

• Barrel Rolls?

Typically at each cardinal heading

• 3 rolls \(\pm 10^\circ\) at 1 Hz
• 3 pitches \(\pm 10^\circ\) at 1 Hz
• 3 yaws \(\pm 10^\circ\) at 1 Hz

(W. E. Tolles and Lawson 1950), (W. E. Tolles 1954), (W. E. Tolles 1955), (A. Gnadt 2022)

Missing from model

• Model is static
• Does not account for changes in time
  • “Permanent” moments can change e.g. temperature dependence
• Does not account for dynamic magnetic sources
  • Electrical use e.g. lights on and off

Machine Learning for MagNav

DAF-MIT AI Accelerator MagNav project

Public Software and Data for MagNav

• https://magnav.mit.edu

• Collected data and made publicly available:

  • https://zenodo.org/record/6327685

• Created software suite published on GitHub:

  • Written in Julia https://juilalang.org
  • https://github.com/MIT-AI-Accelerator/MagNav.jl
  • Docker container https://hub.docker.com/r/jtaylormit/magnav

https://arxiv.org/abs/2007.12158, (A. R. Gnadt et al. 2020)

It can be simple as:

docker run -p 8888:8888 jtaylormit/magnav

Data run-thru

• Collected data made publicly available:
  • https://zenodo.org/record/6327685
  • Hold-out data for challenge problem
• Recorded flight data near Ottawa, ON
  • Position, velocity, attitude (truth)
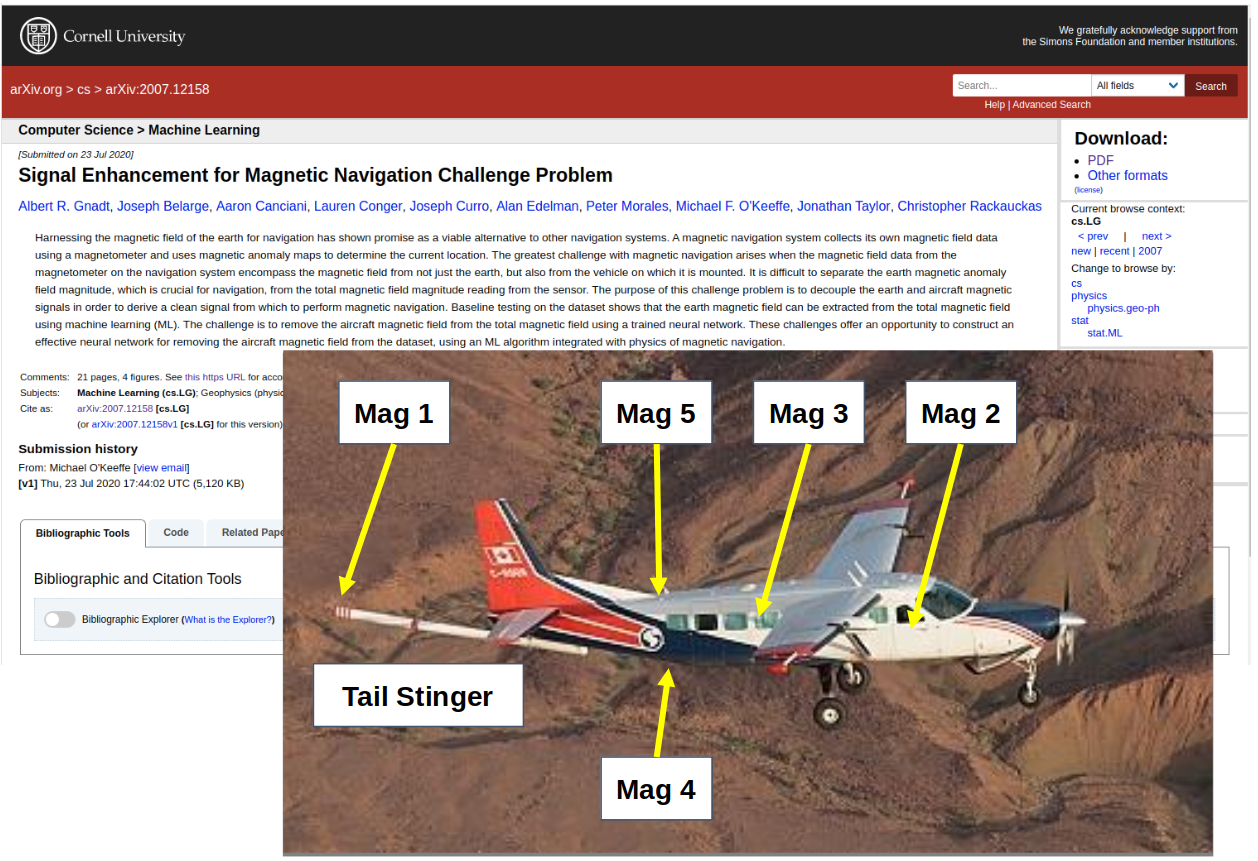
  • Tail Stinger
  • 4 magnetometers in cabin
  • Current and voltage sensors
  • 10 Hz
• Ground station reference sensor
  • 10 Hz
• Magnetic Maps of flight area
• Calibration maneuvers

• Flight crew notes
  • Power lines
  • Railroad tracks
• On-board activities
  • power on/off to systems
  • movement of iron bars
• Professional calibration results

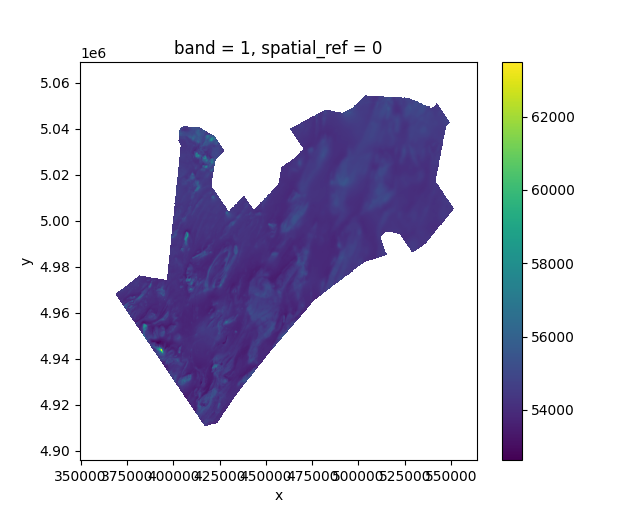
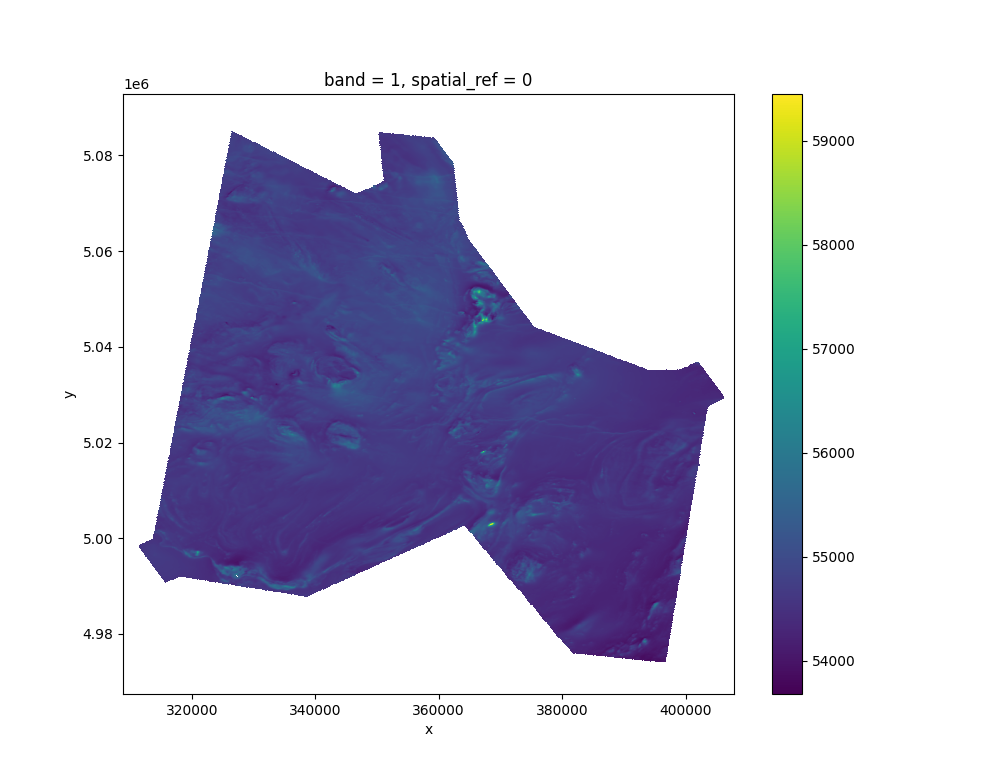
MagNav Software - MagNav.jl

https://github.com/MIT-AI-Accelerator/MagNav.jl

MagNav.jl performance

Software package includes

• Standard Tolles-Lawson
• Neural network calibration options

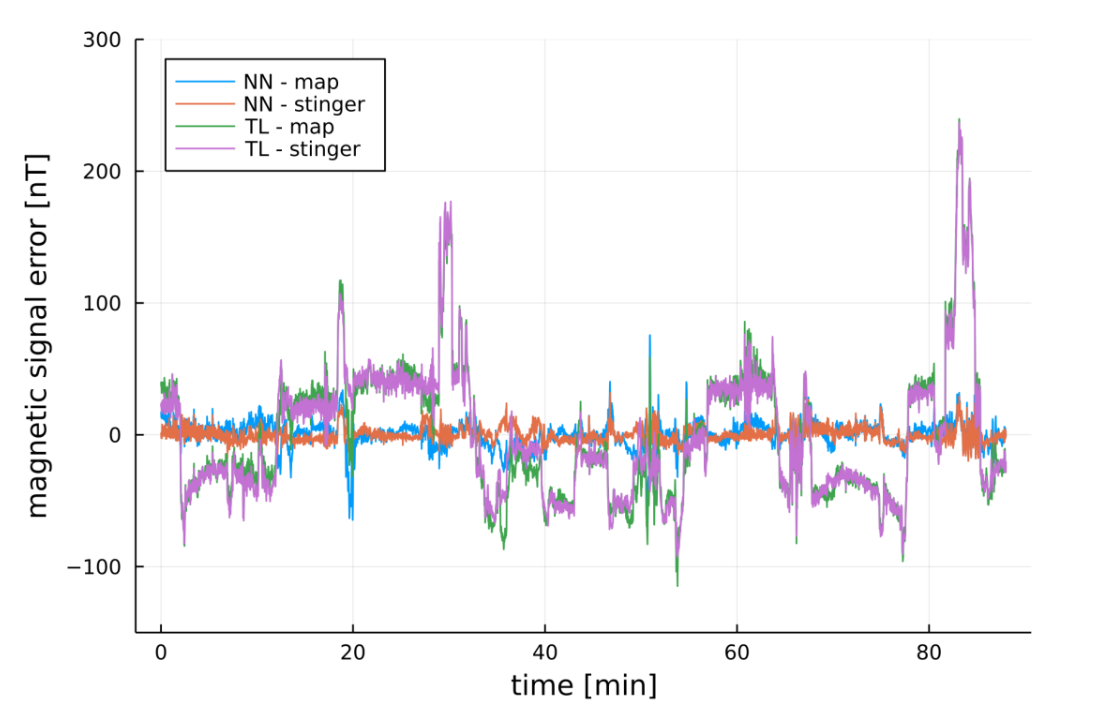
Best in-cabin NN magnetometer performance: \(\sigma=6.32\ \text{nT}\)

(A. R. Gnadt 2022), (A. Gnadt 2022)

Challenge problem

https://magnav.mit.edu

Challenge problem

https://magnav.mit.edu

Arizona State Univ. solution

(Zhai et al. 2023)

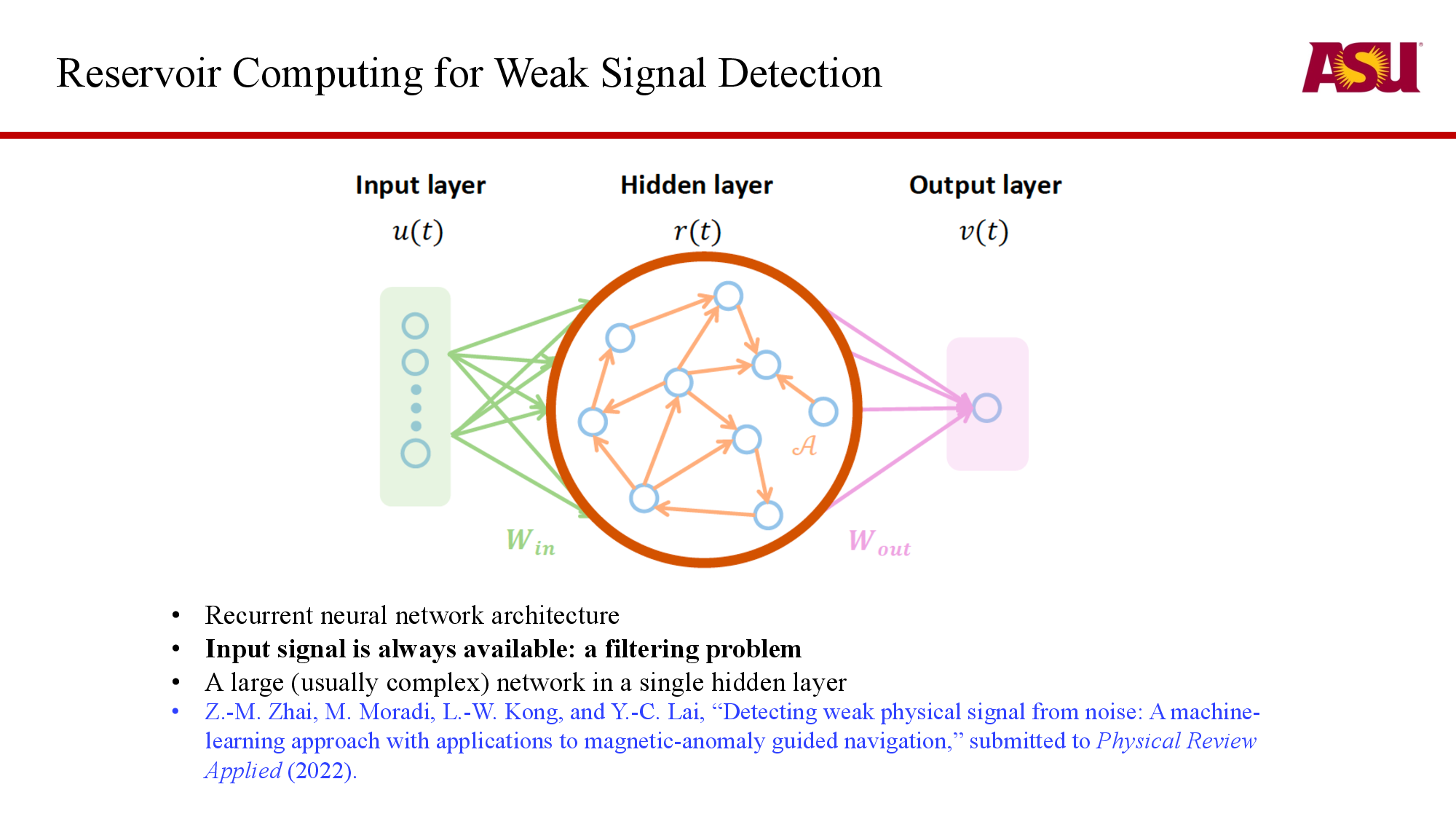
ASU approaches

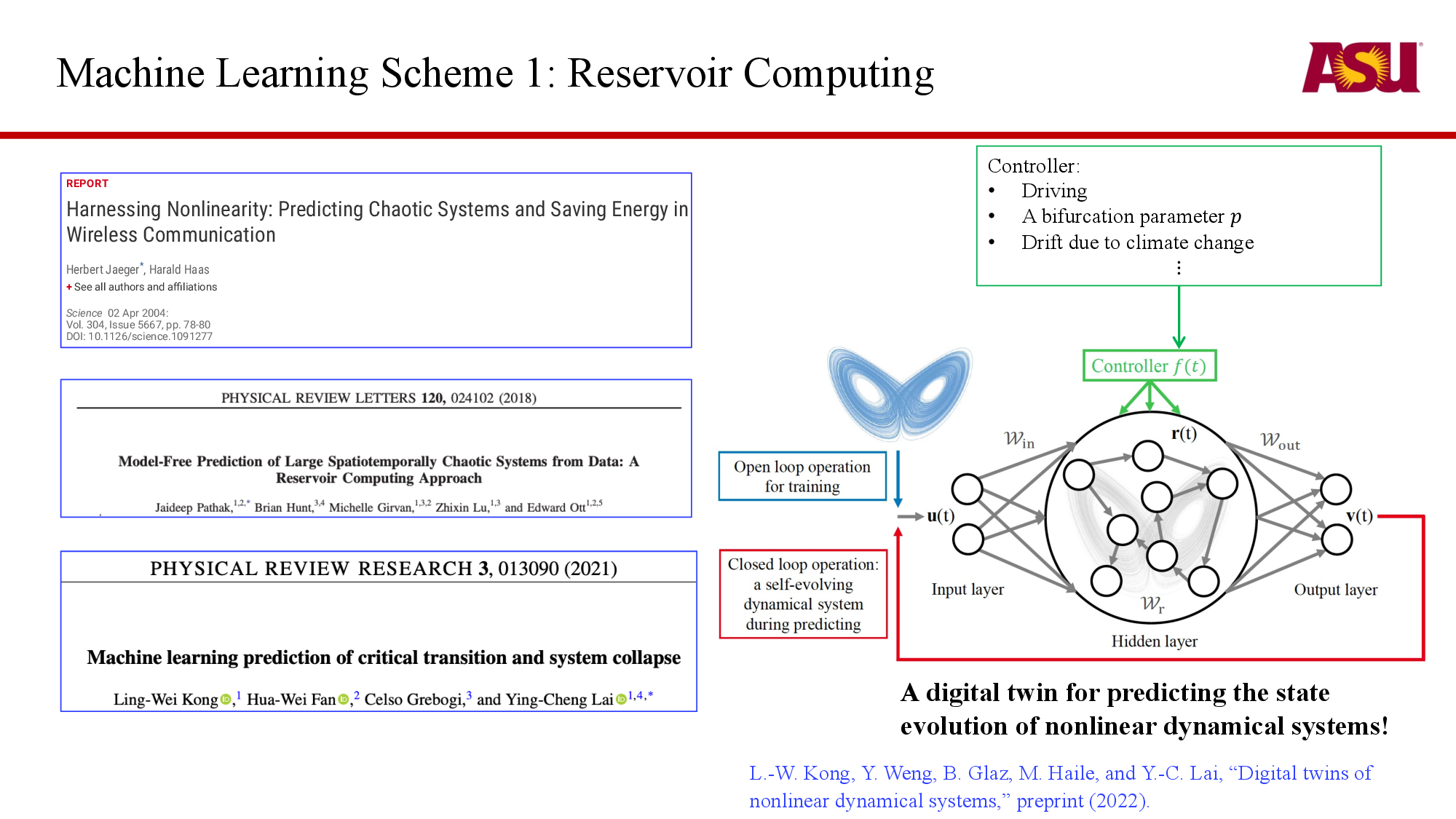
ASU approaches

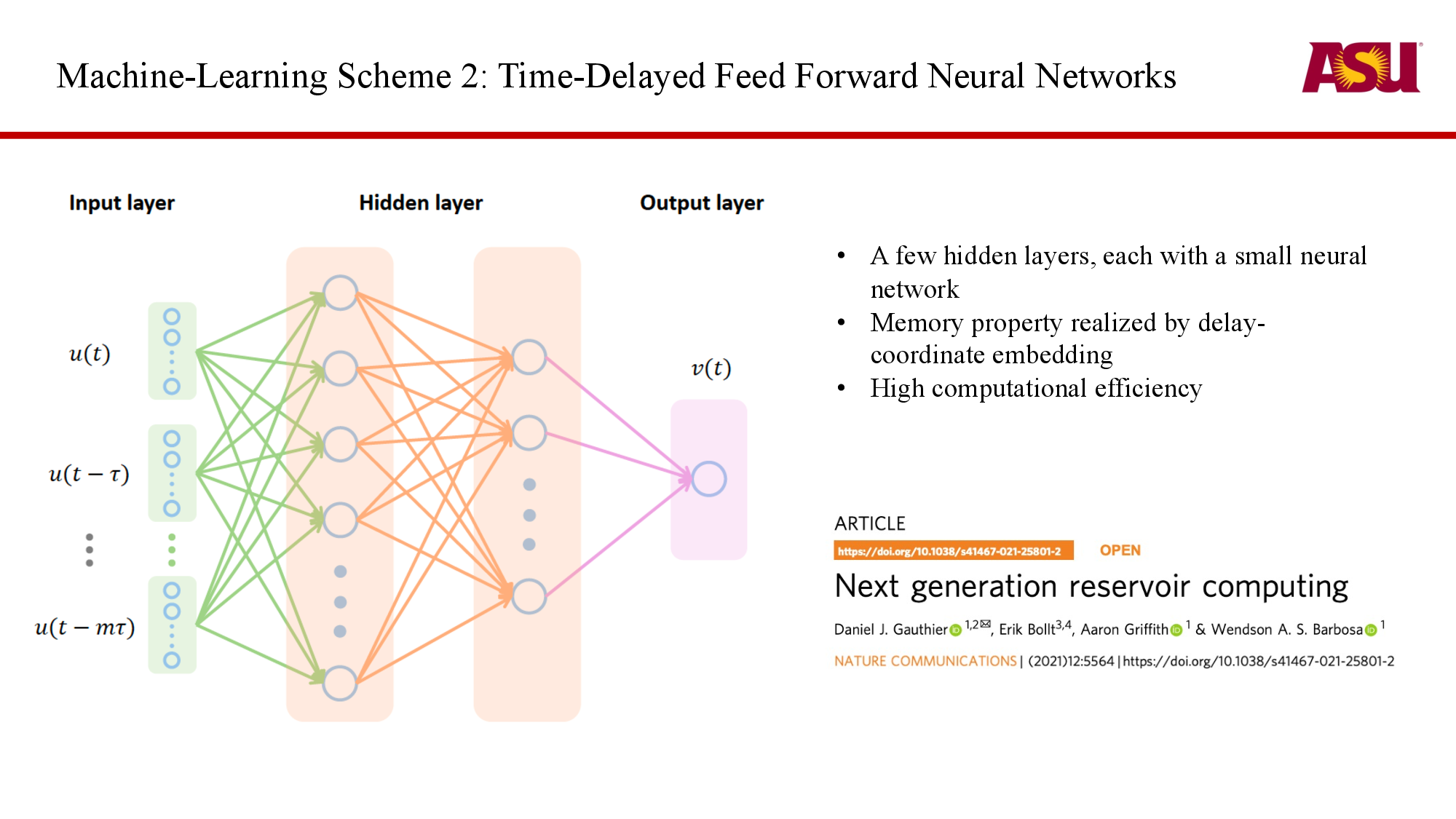
ASU results

\(\sigma\approx\ 4\ \text{nT}\)

Future needs

Future areas for research - maps

• Fill gaps in existing data
• Existing data is low resolution (\(\approx\) 4 km)

Future areas for research - calibration

• Update with payload changes
• Transfer from one vehicle to another

https://www.usgs.gov/media/images/cessna-208b-grand-caravan-1

Thanks

Wright Brothers Institute

Gem City Tech Machine Learning

DAF-MIT AI Acclerator

Contact informaton

Aaron Nielsen, Ph.D.
Autonomy and Navigation Technology Center
Air Force Institute of Technology
Wright-Patterson, AFB, OH

https://www.afit.edu
https://www.afit.edu/ANT
aaron.nielsen.2@au.af.edu

References

Bankey, Viki, Alejandro Cuevas, David Daniels, Carol A. Finn, Israel Hernandez, Patricia Hill, Robert Kucks, et al. 2002. “Digital Data Grids for the Magnetic Anomaly Map of North America.” U.S. Department of the Interior, U.S. Geological Survey; Online; US Geological Survey. https://doi.org/10.3133/ofr02414.

Canciani, Aaron J. 2021. “Magnetic Navigation on an f-16 Aircraft Using Online Calibration.” IEEE Trans. Aerospace and Electronic Systems. https://doi.org/10.1109/TAES.2021.3101567.

Chulliat, A.;W. Brown;P. Alken;C. Beggan;M. Nair;G. Cox;A. Woods;S. Macmillan;B. Meyer;M. Paniccia; 2020. “The US/UK World Magnetic Model for 2020-2025 : Technical Report.” National Centers for Environmental Information (U.S.);British Geological Survey. https://doi.org/10.25923/ytk1-yx35.

Gnadt, Albert. 2022. “Advanced Aeromagnetic Compensation Models for Airborne Magnetic Anomaly Navigation.” PhD thesis, Massachusetts Institute of Technology. https://dspace.mit.edu/handle/1721.1/145137.

Gnadt, Albert R. 2022. “Machine Learning-Enhanced Magnetic Calibration for Airborne Magnetic Anomaly Navigation.” In AIAA SciTech 2022 Forum. https://doi.org/10.2514/6.2022-1760.

Gnadt, Albert R., Joseph Belarge, Aaron Canciani, Glenn Carl, Lauren Conger, Joseph Curro, Alan Edelman, et al. 2020. “Signal Enhancement for Magnetic Navigation Challenge Problem.” arXiv. https://doi.org/10.48550/ARXIV.2007.12158.

Meyer, B., A. Chulliat, and R. Saltus. 2017. “Derivation and Error Analysis of the Earth Magnetic Anomaly Grid at 2 Arc Min Resolution Version 3 (EMAG2v3).” Geochemistry, Geophysics, Geosystems 18 (12): 4522–37. https://doi.org/10.1002/2017gc007280.

Roberts, Carter W., and Robert C. Jachens. 2000. “Preliminary Aeromagnetic Anomaly Map of California.” United States Geologic Survey. https://pubs.usgs.gov/of/1999/0440/.

Tolles, W E, and J D Lawson. 1950. “Magnetic compensation of MAD equipped aircraft.” Airborne Instruments Lab. Inc., Mineola, NY, Rept, 201–1.

Tolles, W. E. 1954. Compensation of aircraft magnetic fields. 2692970, issued 1954.

———. 1955. Magnetic field compensation system. 2706801, issued 1955.

Zhai, Zheng-Meng, Mohammadamin Moradi, Ling-Wei Kong, and Ying-Cheng Lai. 2023. “Detecting Weak Physical Signal from Noise: A Machine-Learning Approach with Applications to Magnetic-Anomaly-Guided Navigation.” Phys. Rev. Applied 19 (March). https://doi.org/10.1103/PhysRevApplied.19.034030.