Navigation

IEEE/ION PLANS 2023, Monterey, CA

Aaron Nielsen

The views expressed in this article are those of the author and do not necessarily reflect the official policy or position of the United States Government, Department of Defense, United States Air Force or Air University.

Distribution A: Authorized for public release. Distribution is unlimited. Case No. 2023-0277.

https://rpubs.com/friendly/test-newcommands https://quarto.org/docs/authoring/markdown-basics.html#equations

https://stackoverflow.com/questions/41362012/how-to-insert-font-awesome-icons-in-mathjax

Font-Awesome will only work for html type output

\[ \newcommand{\dvec}[1]{\dot{\vec{#1}}} \newcommand{\ddvec}[1]{\ddot{\vec{#1}}} \newcommand{\mat}[1]{\mathbf{#1}} \newcommand{\earth}{{\oplus}} \newcommand{\ext}{\text{ext}} \newcommand{\faPlane}{\class{fa fa-plane}{}} \newcommand{\plane}{\class{fa fa-plane}{}} \newcommand{\sensor}{\text{Sensor}} \]

Magnetic Navigation filter

• Uses an Inertial Navigation System (INS)
• Magnetic Navigation is a map-matching process
  • sequential estimation
  • single measurement value compared to map
• Navigator provides error correction to the drifting INS solution
• Kalman filter variant
  • Extended Kalman filter

Navigator overview - Extended Kalman Filter

State vector

\[ \vec{x}= \begin{bmatrix} \smash[b]{\underbrace{\begin{matrix} \delta \vec{p} & \delta \vec{v} & \delta \vec{\epsilon} & \vec{b}_a & \vec{b}_g\end{matrix}}_{\text{Pinson 15}}} & \smash[b]{\underbrace{\begin{matrix}\delta h_a & \delta a\end{matrix}}_{\text{Baro}}} & S_\text{fogm} & S_\text{bias} \end{bmatrix} \]

Measurement processor

\[ z = h(\vec{x}) + v \] \[ h(\vec{x}) = |B_\mathrm{a}| + |B_\text{earth}| + {\color{gray}|B_\text{Plane}}| + S_\text{fogm} + S_\text{bias} \]

Where

• \(|B_\mathrm{a}|\) comes from map interpolation
• \(|B_\text{earth}|\) World Magnetic Model
• \(|B_\text{Plane}|\) aircraft disturbance field - not included here with SGL calibration
• \(S_\text{fogm}\) scalar state estimates of space-weather
• \(S_\text{bias}\) offset bias between map and measurement

Required data sources

• Inertial Navigation System (INS)
  • Angle rates, \(\Delta\theta\)
  • Accelerations/specific forces, \(\Delta\vec{v}\)
• Barometer
  • Precise but not accurate
  • Stablize the altitude
• Magnetometers
  • Scalar - primary sensor
  • Vector - for compensation
• Magnetic Map
  • Core field model e.g. WMM or IGRF
  • Magnetic anomaly map

Kalman filter review

Discrete time dynamics at time index \(k+1\) the state vector \(\vec{x}_{k+1}\) is \[ \vec{x}_{k+1} = {\Phi}_k \vec{x}_k + {B}_k \vec{u}_k + \vec{w}_k \]

• \(\Phi_k\) is the state transition matrix
  
• \(B_k\) is the input or control matrix
  
  • we are not supplying control, so \(B=0\)
    
• \(\vec{w}\sim \mathcal{N}(0,{Q})\) is Gaussian white noise process with covariance matrix \({Q}\)

A measurement \(\vec{z}\) is \[ \vec{z}_k = {H}_k \vec{x}_k + \vec{v}_k \]

• \({H}\) is connection between state \(\vec{x}\) and measurement \(\vec{z}\)
  

• \(\vec{v}\sim\mathcal{N}(0,{R})\) is the noise process of the measurement with covariance \({R}\)

• (Brown and Hwang 2012)

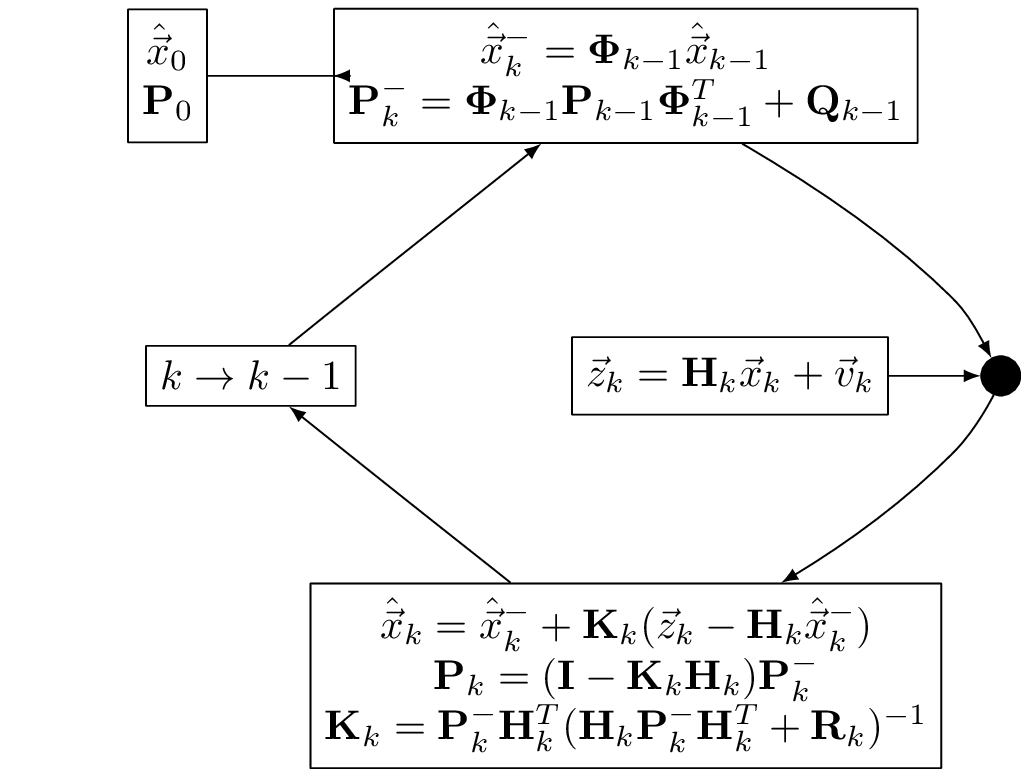
The state \(\vec{x}_{k}\) has a mean \(\hat{\vec{x}}_{k}\) and covariance \({P}_{k}\) which propagates forward in time (with no other information) like: \[ \begin{aligned} \hat{\vec{x}}_{k+1}^- & = {\Phi}_k \hat{\vec{x}}_{k} + \cancelto{0}{{B}\vec{u}_k} \\ {P}_{k+1}^- & = {\Phi}_k {P}_{k} {\Phi}_k^T + {Q}_k \end{aligned} \] When a measurement \(\vec{z}\) is made, we can update the propagated state vector \[ \begin{aligned} \hat{\vec{x}}_{k} &= \hat{\vec{x}}_{k}^- + {K}_k (\vec{z}_k - {H}_k \hat{\vec{x}}_{k}^-)\\ {P}_k &= ({I} -{K}_k {H}_k ) {P}_{k}^- \\ {K}_k &= {P}_{k}^- {H}_k^T( {H}_k {P}_{k}^- {H}_k^T + {R}_k )^{-1} \end{aligned} \]

Kalman filter flow diagram

Linearization for navigation

The map-matching measurement processor is non-linear. Two primary approaches have been used for MagNav:

• Extended Kalman Filter (EKF) (Mount 2018), (Clarke 2021), (Canciani 2021), (McNeil 2022)
• Rao-Blackwellized (or marginalized) Particle Filter (RBPF) (Canciani 2016)
  EKF seems to work most of the time
  

Linearization of Kalman filter

Generalize the state dynamics and measurement \[ \begin{aligned} \dvec{x} & = \vec{f}(\vec{x}, \vec{u}_d, t) + \vec{u}(t) \\ \vec{z} & = \vec{h}(\vec{x}, t) + \vec{v}(t) \end{aligned} \]

• \(\vec{f}(\vec{x}, \vec{u}_d, t)\) and \(\vec{h}(\vec{x}, t)\) are known functions
• \(\vec{u}_d\) deterministic forcing function (e.g. gravity)
• \(\vec{u}\) and \(\vec{v}\) are uncorrelated white noise processes

Write the state \(\vec{x}\) in terms of some \(\vec{x}^*(t)\) and a deviation from it \(\Delta\vec{x}(t)\) \[ \vec{x}(t) = \vec{x}^*(t) + \Delta\vec{x}(t) \]

Linearization of Kalman filter

\[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & = \vec{f}(\vec{x}^* + \Delta\vec{x}, \vec{u}_d, t) + \vec{u}(t) \\ \vec{z} & = \vec{h}(\vec{x}^* +\Delta\vec{x}, t) + \vec{v}(t) \end{aligned} \]

\(\Delta\vec{x}\) is small and use Taylor series (so many Taylor series) \[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & \approx \vec{f}(\vec{x}^*, \vec{u}_d, t) + \left[ \frac{\partial \vec{f}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{u}(t) \\ \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \] If \(\vec{x}^*\) is just a single known trajectory, then this is just the Linearized Kalman filter.

If \(\vec{x}^*\) is our trajectory estimate, then this is the Extended Kalman filter.

Equivalent linearized represenation

\[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & \approx \vec{f}(\vec{x}^*, \vec{u}_d, t) + \left[ \frac{\partial \vec{f}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{u}(t) \\ \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \] Becomes \[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & \approx \vec{f}(\vec{x}^*, \vec{u}_d, t) + \mat{F} \cdot \Delta\vec{x} + \vec{u}(t) \\ \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \mat{H} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \] with \[ \mat{F} = \left[ \frac{\partial \vec{f}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*},\ \mat{H} = \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \]

Extended Kalman Filter (EKF)

Write the linearized measurement as \[ \vec{z} - \vec{h}(\vec{x}^*) = \mat{H} \Delta \vec{x} + \vec{v} \] The incremental estimate update at time \(t_k\) is \[ \Delta\hat{\vec{x}}_k = \Delta\hat{\vec{x}}_k^- + \mat{K}_k \left[ \vec{z}_k - \vec{h}(\vec{x}^*_k) - \mat{H}_k \Delta\hat{\vec{x}}_k^- \right] \] Write the estimate of what the measurement should be \[ \hat{\vec{z}}^-_k = \vec{h}(\vec{x}^*_k) + \mat{H}_k \Delta\hat{\vec{x}}_k^- \] And then \[ \underbrace{\vec{x}^*_k + \Delta\hat{\vec{x}}_k}_{\textstyle\hat{\vec{x}}_k} = \underbrace{\vec{x}^*_k + \Delta\hat{\vec{x}}_k^-}_{\textstyle\hat{\vec{x}}_k^-} + \mat{K}_k \left[ \vec{z}_k - \hat{\vec{z}}^-_k \right] \]

EKF data flow

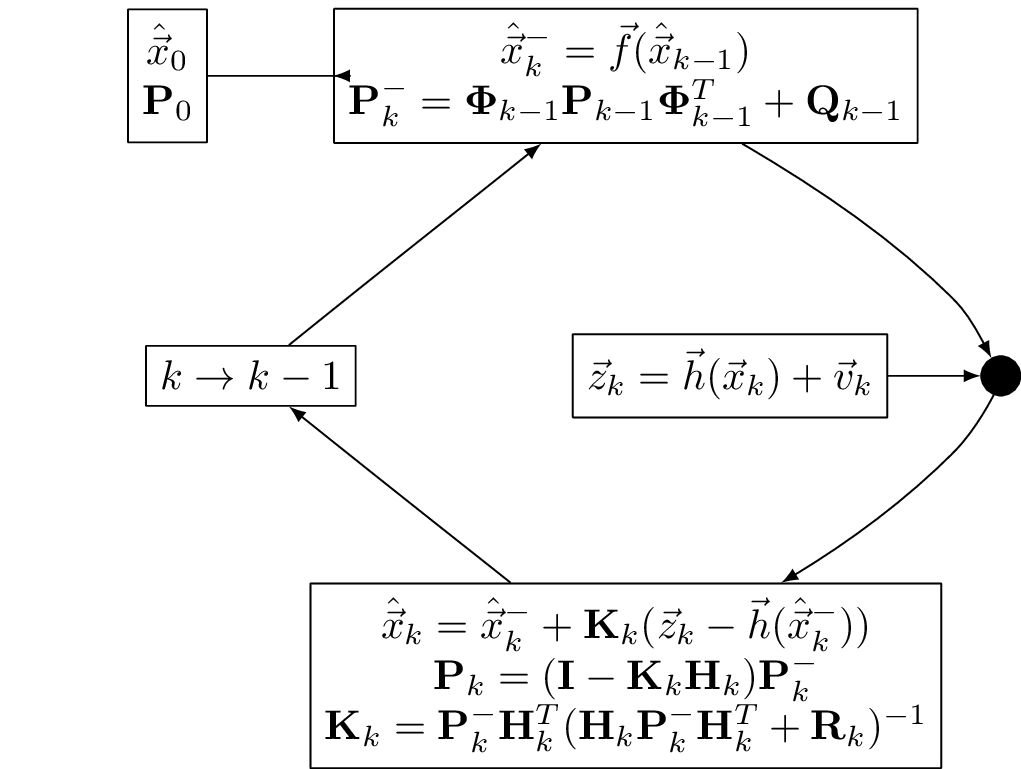
Pinson-9 model for inertial navigation

(Titterton and Weston 2004), (Raquet 2021)

Pinson 9-state model for INS is: \[ \vec{x} = \begin{bmatrix} \delta x_n \\ \delta x_e \\ \delta x_d \\ \delta v_n \\ \delta v_e \\ \delta v_d \\ \delta\epsilon_n \\ \delta\epsilon_e \\ \delta\epsilon_d \\ \end{bmatrix} = \begin{bmatrix} \delta\vec{x} \\ \delta\vec{v} \\ \delta\vec{\epsilon} \\ \end{bmatrix} \]

Where:

• \(\delta\vec{x}\) are the NED position error states
• \(\delta\vec{v}\) are the NED velocity error states
• \(\delta\vec{\epsilon}\) are the angle atittude errors

and \[ \dvec{x} = \mat{F} \vec{x} \]

Pinson-9 model propagation

\[ \begin{bmatrix} \delta\dvec{x} \\ \delta\dvec{v} \\ \delta\dvec{\epsilon} \end{bmatrix} = \begin{bmatrix} F_{xx} & F_{xv} & F_{x\epsilon} \\ F_{vx} & F_{vv} & F_{v\epsilon} \\ F_{\epsilon x} & F_{\epsilon v} & F_{\epsilon \epsilon} \\ \end{bmatrix} \begin{bmatrix} \delta \vec{x} \\ \delta \vec{v} \\ \delta \vec{\epsilon} \\ \end{bmatrix} \] We are working in geodetic coordinates so the elements of \(\mat{F}\) depend upon Earth specifc parameters to account for Coriolis force.

Pinson-9 model propagation definitions

Variable	Description	Value/Units
\(\phi\)	latitude	radian
\(v_n\)	north velocity	meter/second
\(v_e\)	east velocity	meter/second
\(v_d\)	down velocity	meter/second
\(f_n\)	north specific force	meter/second/second
\(f_e\)	east specific force	meter/second/second
\(f_d\)	down specific force	meter/second/second
\(R_\earth\)	Earth radius	635300 meter
\(\Omega_\earth\)	Earth rotation rate	7.2921151467e-5/second

Components of \(\mat{F}\), \(F_x\) row

\[ F_{xx} = \begin{bmatrix} 0 & 0 & -\frac{v_n}{R_\earth^2}\\ \frac{v_e \tan \phi}{R_\earth\cos \phi} & 0 & \frac{v_e}{R_\earth^2 \cos\phi} \\ 0 & 0 & 0 \\ \end{bmatrix} \]

\[ F_{xv} = \begin{bmatrix} \frac{1}{R_\earth} & 0 & 0\\ 0 & \frac{1}{R_\earth\cos\phi} & 0 \\ 0 & 0 & -1 \\ \end{bmatrix} \]

\[ F_{x\epsilon} = \mat{0}_{3\times 3} \]

\(F_v\) row of \(\mat{F}\)

\[ F_{vx} = \begin{bmatrix} v_e \left( 2\Omega_\earth\cos\phi + \frac{v_e}{R_\earth\cos^2\phi} \right) & 0 & \frac{v_e^2\tan\phi - v_n v_d}{R_\earth^2}\\ 2\Omega_\earth \left(v_n \cos\phi - v_d \sin\phi\right) + \frac{v_n v_e}{R_\earth \cos^2\phi} & 0 & \frac{-v_e (v_n\tan\phi +v_d)}{R_\earth^2}\\ 2\Omega_\earth v_e \sin \phi & 0 & \frac{v_n^2 + v_e^2}{R_\earth} \\ \end{bmatrix} \]

\[ F_{vv} = \begin{bmatrix} \frac{v_d}{R_\earth} & -2 \left( \Omega_\earth \sin\phi + \frac{v_e\tan\phi}{R_\earth} \right) & \frac{v_n}{R_\earth} \\ 2\Omega_\earth\sin\phi + \frac{v_e\tan\phi}{R_\earth} & \frac{v_n\tan\phi+v_d}{R_\earth} & 2\Omega_\earth \cos\phi + \frac{v_e}{R_\earth} \\ -\frac{2v_n}{R_\earth} & -2 \left( \Omega_\earth \cos\phi + \frac{v_e}{R_\earth} \right) & 0 \\ \end{bmatrix} \]

\[ F_{v\epsilon} = \begin{bmatrix} 0 & -f_d & f_e \\ f_d & 0 & -f_n \\ -f_e & f_n & 0 \end{bmatrix} \]

\(F_\epsilon\) row of \(\mat{F}\)

\[ F_{\epsilon x} = \begin{bmatrix} -\Omega_\earth \sin\phi & 0 & -\frac{v_e}{R_\earth} \\ 0 & 0 & \frac{v_n}{R_\earth^2} \\ -\Omega_\earth \cos\phi - \frac{v_e}{R_\earth \cos^2\phi} & 0 & \frac{v_e\tan\phi}{R_\earth^2} \end{bmatrix} \]

\[ F_{\epsilon v } = \begin{bmatrix} 0 & 1/R_\earth & 0 \\ -1/R_\earth & 0 & 0 \\ 0 & \frac{\tan\phi}{R_\earth} & 0 \\ \end{bmatrix} \]

\[ F_{\epsilon\epsilon} = \begin{bmatrix} 0 & -\Omega_\earth\sin\phi + \frac{v_e}{R_\earth\tan\phi} & v_n/R_\earth \\ \Omega_\earth\sin\phi + \frac{v_e\tan\phi}{R_\earth} & 0 & \Omega_\earth\cos\phi + v_e/R_\earth \\ -v_n/R_\earth & -\Omega\cos\phi -v_e/R_\earth & 0 \\ \end{bmatrix} \]

Pinson-15 state model

• Extends the 9-state model to include
• accelerometer \(\vec{b_a}\) and gyro \(\vec{b_g}\) biases
• using First Order Gauss Markov model (FOGM)

\[ \vec{x} = \begin{bmatrix} \delta x_n \\ \delta x_e \\ \delta x_d \\ \delta v_n \\ \delta v_e \\ \delta v_d \\ \delta\epsilon_n \\ \delta\epsilon_e \\ \delta\epsilon_d \\ b_{a_x} \\ b_{a_y} \\ b_{a_z} \\ b_{g_x} \\ b_{g_y} \\ b_{g_z} \\ \end{bmatrix} = \begin{bmatrix} \delta\vec{x} \\ \delta\vec{v} \\ \delta\vec{\epsilon} \\ \vec{b_a}\\ \vec{b_g}\\ \end{bmatrix} \]

Propagation for 15-state Pinson model

\[ \begin{bmatrix} \delta\dvec{x} \\ \delta\dvec{v} \\ \delta\dvec{\epsilon} \\ \dvec{b_a}\\ \dvec{b_g}\\ \end{bmatrix} = \begin{bmatrix} F_{xx} & F_{xv} & 0 & 0 & 0\\ F_{vx} & F_{vv} & F_{v\epsilon} & \mat{C}_b^n & 0 \\ F_{\epsilon x} & F_{\epsilon v} & F_{\epsilon \epsilon} & 0 & -\mat{C}_b^n \\ 0 & 0 & 0 & F_{aa} & 0 \\ 0 & 0 & 0 & 0 & F_{gg} \\ \end{bmatrix} \begin{bmatrix} \delta \vec{x} \\ \delta \vec{v} \\ \delta \vec{\epsilon} \\ \vec{b}_a\\ \vec{b}_g\\ \end{bmatrix} \]

\[ F_{aa} = \begin{bmatrix} -1/\tau_a & 0 & 0 \\ 0 & -1/\tau_a & 0 \\ 0 & 0 & -1/\tau_a\\ \end{bmatrix},\ F_{gg} = \begin{bmatrix} -1/\tau_g & 0 & 0 \\ 0 & -1/\tau_g & 0 \\ 0 & 0 & -1/\tau_g\\ \end{bmatrix} \] and \(\mat{C}_b^n\) is the direction cosine matrix that rotates from body to NED frame.

MagNav additions to Pinson-15

• Add a barometer altimeter to constrain Altitude
  • \(\delta h_a\) is the altitude error correction to the INS
  • \(\delta a\) is the vertical acceleration error (we already have \(\delta v_n\) in Pinson-9)
• Add a state \(S\) to model external time-correlated magnetic field variations
  • space weather
  • effects must be out-side of navigation frequency band

Results in an 18-component state vector \[ \begin{bmatrix} \delta \vec{x} & \delta \vec{v} & \delta \vec{\epsilon} & \vec{b}_a & \vec{b}_g & \delta h_a & \delta a & S \end{bmatrix} \]

Updates to \(\mat{F}\) matrix

\[ \begin{bmatrix} \delta\dvec{x} \\ \delta\dvec{v} \\ \delta\dvec{\epsilon} \\ \dvec{b}_a\\ \dvec{b}_g\\ \dot{h_a}\\ \dot{\delta_a}\\ \dot{S} \end{bmatrix} = \begin{bmatrix} F_{xx} & F_{xv} & 0 & 0 & 0 & F_{xb} & 0 \\ F_{vx} & F_{vv} & F_{v\epsilon} & \mat{C}_b^n & 0 & F_{vb} & 0 \\ F_{\epsilon x} & F_{\epsilon v} & F_{\epsilon \epsilon} & 0 & -\mat{C}_b^n & 0 & 0 \\ 0 & 0 & 0 & F_{aa} & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & F_{gg} &0 & 0 \\ F_{bp} & 0 & 0 & 0 & 0 & F_{bb} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & F_{ss} \\ \end{bmatrix} \begin{bmatrix} \delta \vec{x} \\ \delta \vec{v} \\ \delta \vec{\epsilon} \\ \vec{b}_a\\ \vec{b}_g\\ \delta h_a \\ \delta a \\ S \end{bmatrix} \]

Updated \(\mat{F}\) components

Barometer aiding: \[ \mat{F}_{xb} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ k_1 & 0 \end{bmatrix},\ \mat{F}_{vb} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ -k_2 & 1 \\ \end{bmatrix} \]

\[ \mat{F}_{bx} = \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & k_3 \\ \end{bmatrix},\ \mat{F}_{bb} = \begin{bmatrix} -\frac{1}{\tau_b} & 0 \\ -k_3 & 0 \\ \end{bmatrix} \]

The space weather, diurnal bias is given by: \[ \mat{F}_{ss} = \frac{1}{\tau_s} \]

MagNav measurement processor

The scalar sensor measures: \[ |\vec{B}_\text{total}| = |\vec{B}_\ext + \vec{B}_\text{\faPlane} | \] and \[ \vec{B}_\ext = \vec{B}_\earth+ \vec{B}_\text{anomaly} + \vec{B}_\text{disturbance} \]

• We added a state \(S\) into the MagNav model to account for \(\vec{B}_\text{disturbance}\).
• \(\vec{B}_\earth\) from IGRF or WMM
  • Both IGRF and WMM are functions of lat, long, altitude and time
  • WMM has \(28.8^\circ\) or 3200 km at surface resolution
  • Secular variaton \(\approx 100 \text{nT}/\text{year} = 0.27 \text{nT}/\text{day}\)

MagNav Measurement Processor \(H\) matrix

\[ \begin{aligned} \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \mat{H} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \]

\[ \mat{H} = \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \]

\[ \mat{H}(\vec{x}^*) = \begin{bmatrix} \frac{\partial h(\vec{x}^*)}{\partial x_n} \\ \frac{\partial h(\vec{x}^*)}{\partial x_e} \\ \frac{\partial h(\vec{x}^*)}{\partial x_d} \\ \mat{0}_{1x15} \end{bmatrix} \leftarrow\text{This is the gradient of the map} \] Both the map and 3D gradient of the map are needed in order to make a measurement and incorporate it.

Navigation pre-processor

• Prepare Magnetic Anomaly Map
  • Upward continue as needed for flight altitudes
  • Compute 3-D gradient for measurement processor
• Precompute Core field model as needed
• Prepare Tolles-Lawson Compensation coefficients
  • In an adaptive or online calibration this is a starting point

Filter initialization

• Assume known starting value for position and attitude from GPS-aided system
  • Tolles-Lawson coefficients are needed
• Works well for EKF - provides excellent starting point for state
  • State starting point initializes map error state \(S\)
• Particle filter initialization
  • Randomly draw ensemble of \(N\) particles from my anticpated distribution
  • This includes a position \(\vec{x}\) and map bias \(S\) hypothesis

Brown, Robert Grover, and Patrick Y C Hwang. 2012. Introduction to random signals and applied kalman filtering: with MATLAB exercises and solutions; 4th ed. New York, NY: Wiley.

Canciani, Aaron J. 2016. “Absolute Positioning Using the Earth’s Magnetic Field.” PhD thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/251.

———. 2021. “Magnetic Navigation on an f-16 Aircraft Using Online Calibration.” IEEE Trans. Aerospace and Electronic Systems. https://doi.org/10.1109/TAES.2021.3101567.

Clarke, Daniel J. 2021. “Real-Time Aerial Magnetic and Vision-Aided Navigation.” Master’s thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/4994/.

Gelb, Arthur et al. 1974. Applied Optimal Estimation. MIT press.

McNeil, Alexander J. 2022. “Magnetic Anomaly Absolute Positioning for Hypersonic Aircraft.” Master’s thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/5457.

Mount, Lauren A. 2018. “Navigation Using Vector and Tensor Measurements of the Earth’s Magnetic Anomaly Field.” Master’s thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/1817/.

Raquet, John. 2021. “Pinson 15 Model.”

Titterton, David, and John Weston. 2004. Strapdown Inertial Navigation Technology. Institution of Engineering; Technology. https://doi.org/dx.doi.org/10.1049/PBRA017E.