Tolles-Lawson Compensation

IEEE/ION PLANS 2023, Monterey, CA

Aaron Nielsen

The views expressed in this article are those of the author and do not necessarily reflect the official policy or position of the United States Government, Department of Defense, United States Air Force or Air University.

Distribution A: Authorized for public release. Distribution is unlimited. Case No. 2023-0277.

https://rpubs.com/friendly/test-newcommands https://quarto.org/docs/authoring/markdown-basics.html#equations

https://stackoverflow.com/questions/41362012/how-to-insert-font-awesome-icons-in-mathjax

Font-Awesome will only work for html type output

\[ \newcommand{\dvec}[1]{\dot{\vec{#1}}} \newcommand{\ddvec}[1]{\ddot{\vec{#1}}} \newcommand{\mat}[1]{\mathbf{#1}} \newcommand{\earth}{{\oplus}} \newcommand{\ext}{\text{ext}} \newcommand{\faPlane}{\class{fa fa-plane}{}} \newcommand{\plane}{\class{fa fa-plane}{}} \newcommand{\sensor}{\text{Sensor}} \]

Tolles-Lawson

• Calibration technique developed in WW2 for submarine hunting
• Declassified in 1950’s and patented
• Standard calibration technique used for aero-magnetic surveys
  • Developed by (Leliak 1961)

\[ \begin{align*} |B_\mathrm{Sensor}| &= |\vec{B}_\ext + \vec{B}_\faPlane|\\ &= \sqrt{ |B_\ext|^2 + |B_\faPlane|^2 + 2 |B_\ext||B_\faPlane|\cos\theta}\\ |B_\text{Sensor}| &= |B_\ext| \sqrt{ 1 + \frac{|B_\faPlane|^2}{|B_\ext|^2} + 2\frac{|B_\faPlane|}{|B_\ext|}\cos\theta} \end{align*} \]

Tolles-Lawson Path to Calibration 1/2

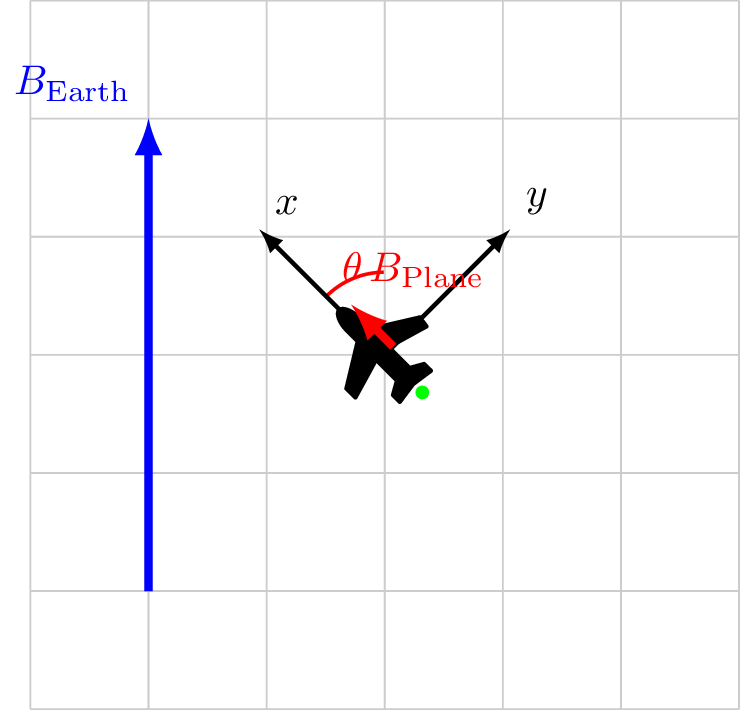
\[ \begin{align*} |B_\text{Sensor}| &= |\vec{B}_\ext + \vec{B}_\faPlane|\\ &= \sqrt{ |B_\ext|^2 + |B_\faPlane|^2 + 2 |B_\ext||B_\faPlane|\cos\theta}\\ |B_\text{Sensor}| &= |B_\ext| \sqrt{ 1 + 2\frac{|B_\faPlane|}{|B_\ext|}\cos\theta}\\ &\approx |B_\ext| + |B_\faPlane|\cos\theta + \cdots \end{align*} \]

Path to Calibration
Measure \(\cos\theta\)

Solve \(|B_\text{sensor}| = |B_\ext| + |B_\plane|\cos\theta\)

Assuming \(|B_\ext|\) is known or constant

Tolles-Lawson Path to Calibration 2/2

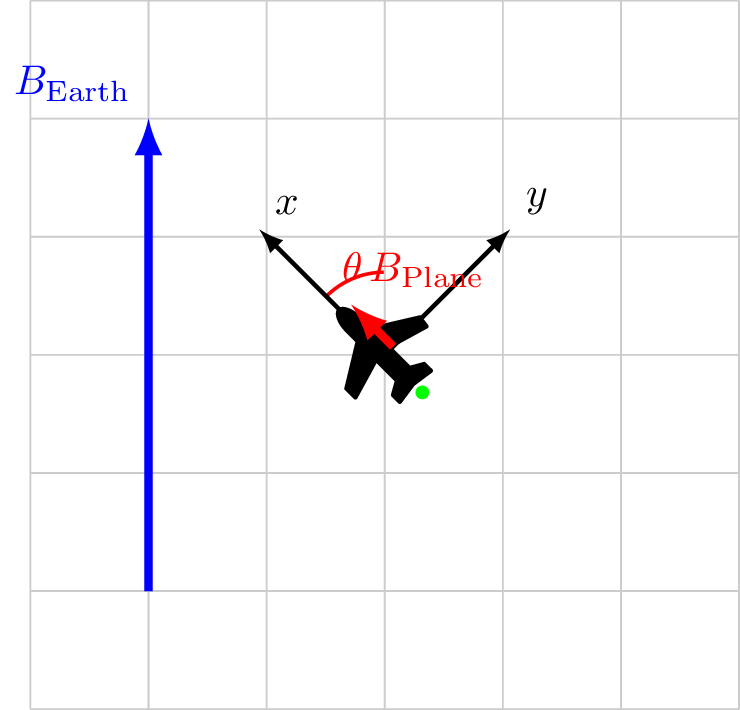
Path to Calibration
Measure \(\cos\theta\)

Solve \(|B_\text{sensor}| = |B_\ext| + |B_\faPlane|\cos\theta\)

Assuming \(|B_\ext|\) is known or constant


How to measure \(\cos\theta\)?
Use a vector magnetometer

Rotate aircraft in \(|B_\ext|\)

Compute direction cosines…

Direction cosines

• The direction cosines are computed in the vector magnetometer reference frame
• The magnetometer is fixed to aircraft body reference frame \[ \begin{aligned} \cos X = & \frac{B_x}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Y = & \frac{B_y}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Z = & \frac{B_z}{\sqrt{B_x^2 + B_y^2 + B_z^2}} \end{aligned} \]

In the 2-D example, \(B_z = 0\)

Calibration 1/4

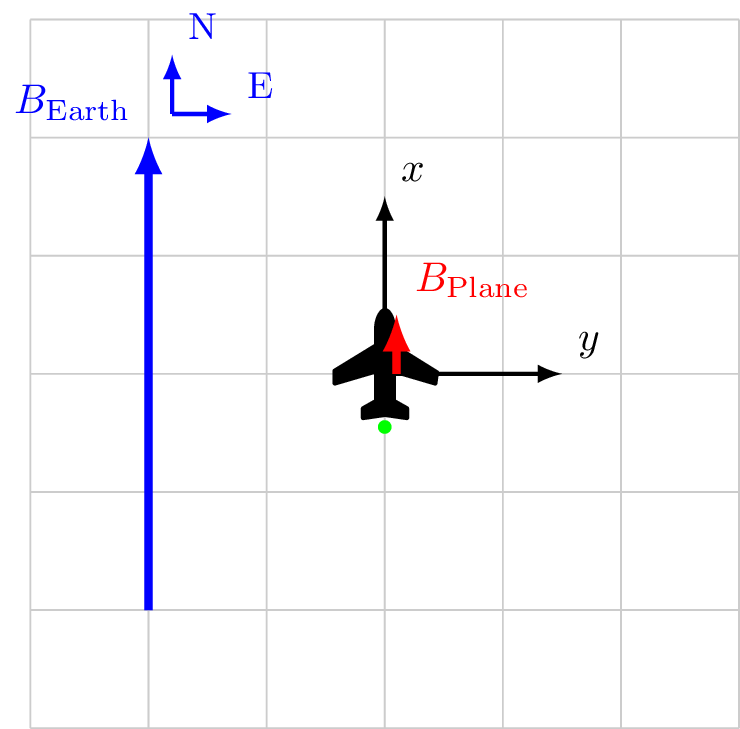
Coordinate system fixed to aircraft
\[\vec{B}_\mathrm{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= 4.0 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && +0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= 4.5 \hat{x} && + 0.0 \hat{y} \\ |B_\text{Sensor}| &= 4.5 && \\ \cos X &= \frac{4.5}{4.5} && = 1\\ \cos Y &= \frac{0.0}{4.5} && = 0\\ \end{alignat*} \]

Calibration 2/4

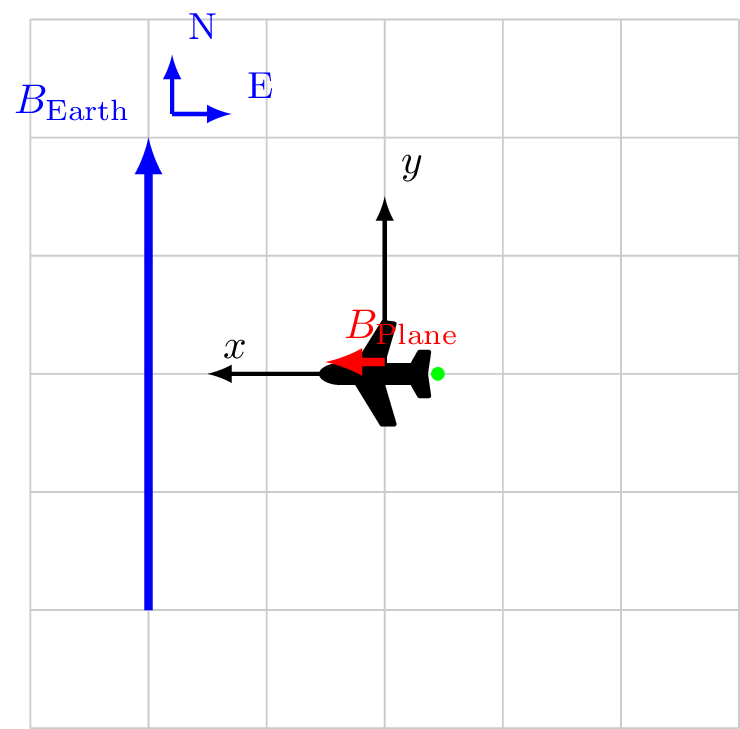
Coordinate system fixed to aircraft
\[\vec{B}_\text{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= 0.0 \hat{x} && + 4.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= 0.5 \hat{x} && + 4.0 \hat{y} \\ |B_\text{Sensor}| &= 4.007 && \\ \cos X &= \frac{0.5}{4.007} && \ne 0 \rightarrow 82.8^\circ\\ \cos Y &= \frac{4.0}{4.007} && \approx 1\\ \end{alignat*} \]

Calibration 3/4

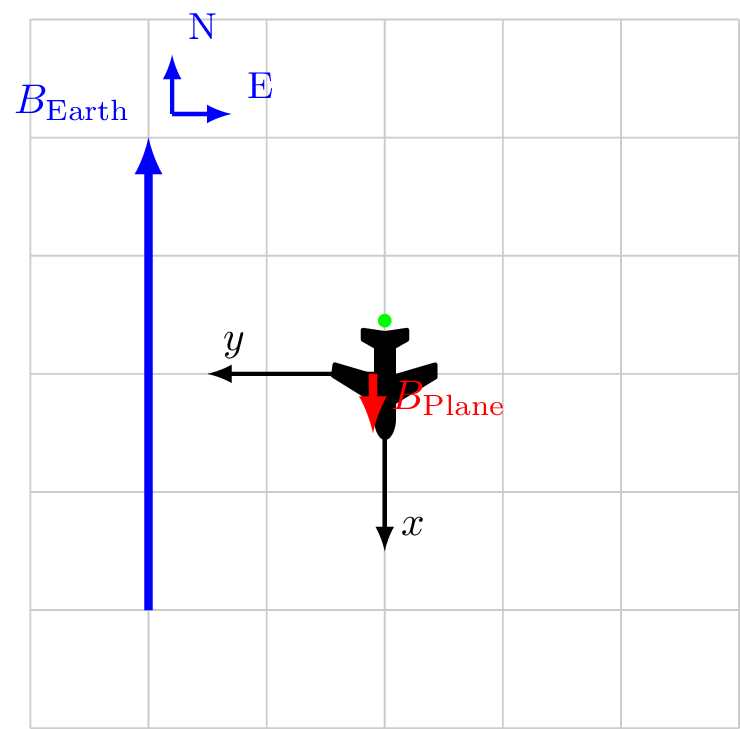
Coordinate system fixed to aircraft
\[\vec{B}_\text{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= -4.0 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= -3.5 \hat{x} && + 0.0 \hat{y} \\ |B_\text{Sensor}| &= 3.5 && \\ \cos X &= \frac{-3.5}{3.5} && = -1\\ \cos Y &= \frac{0}{3.5} && = 0\\ \end{alignat*} \]

Calibration 4/4

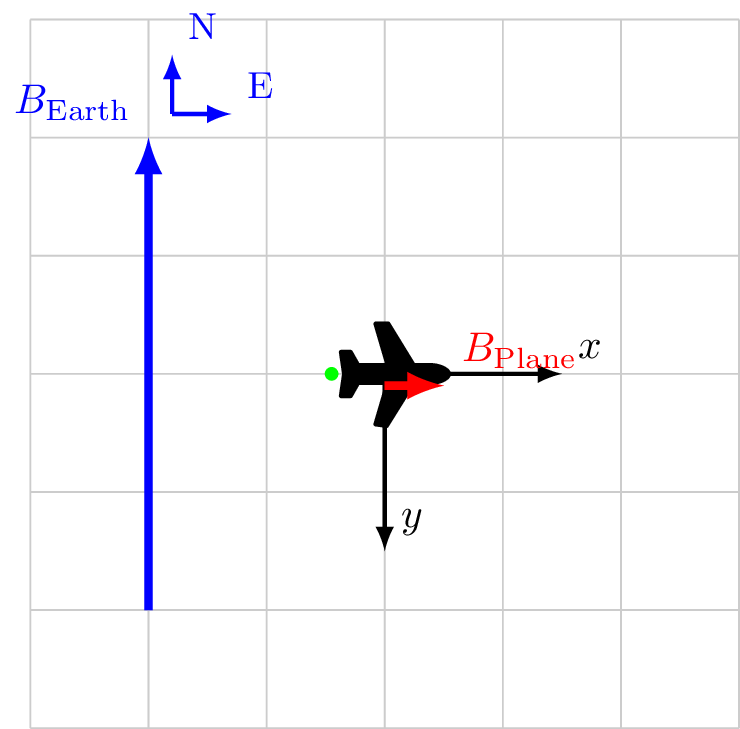
Coordinate system fixed to aircraft
\[\vec{B}_\text{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= 0.0 \hat{x} && + -4.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= 0.5 \hat{x} && + -4.0 \hat{y} \\ |B_\text{Sensor}| &= 4.007 &&\\ \cos X &= \frac{0.5}{4.007} && \ne 0\\ \cos Y &= \frac{-4.0}{4.007} && \approx -1\\ \end{alignat*} \]

Standard calibration model

\[|\vec{B}| = |\vec{B}_\ext + \vec{B}_\faPlane|\]

\[ \begin{array}{ l B c B c B c } \vec{B}_\faPlane & = & \vec{B}_\text{Permanent} & + & \vec{B}_\text{Induced} & + & \vec{B}_\text{Eddy}\\ & = & \vec{P}_\text{constant} {} & + &{} M_{3\times3} \vec{B }_\ext {} & + & {} S_{3\times3} \frac{\partial}{\partial t} \vec{B}_\ext \end{array} \]

\(M_{3\times3}\) is symmetric \(\rightarrow\) 6 independent elements

Total of 18 elements

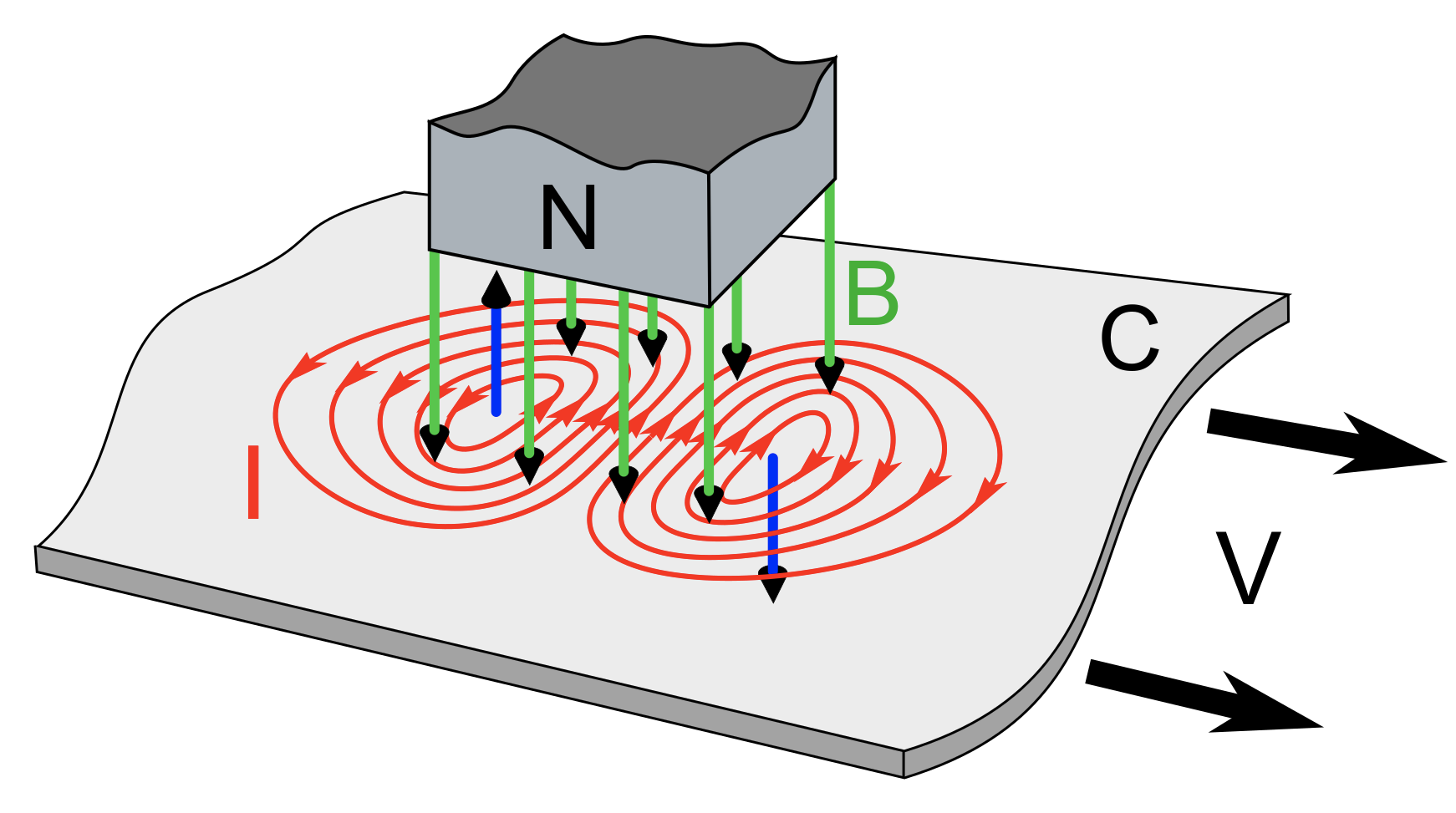
Use the same direction cosines, now with \(B_z\)

The direction cosines are computed from the vector magnetometer

\[ \begin{aligned} \cos X = & \frac{B_x}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Y = & \frac{B_y}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Z = & \frac{B_z}{\sqrt{B_x^2 + B_y^2 + B_z^2}} \end{aligned} \]

Tolles-Lawson full implementation

\[ \begin{aligned} B_\plane & = & & { c_1 \cos X + c_2 \cos Y + c_3 \cos Z }+ \\ & & B_\ext & {[ c_4 \cos^2 X + c_5 \cos X \cos Y + c_6 \cos X \cos Z +} \\ & & & { c_7 \cos^2 Y + c_8 \cos Y \cos Z + c_9 \cos^2 Z ] + } \\ & & B_\ext & { [ c_{10} \cos X \cos' X + c_{11} \cos X \cos' Y + c_{12} \cos X \cos' Z }+ \\ & & & { c_{13} \cos Y \cos' X + c_{14} \cos Y \cos' Y + c_{15} \cos Y \cos' Z +} \\ & & & { c_{16} \cos Z \cos' X + c_{17} \cos Z \cos' Y + c_{18} \cos Z \cos' Z ] } \end{aligned} \]

We need a method to solve for \(c_1 \ldots c_{18}\)

How to sample the range of possible angles?

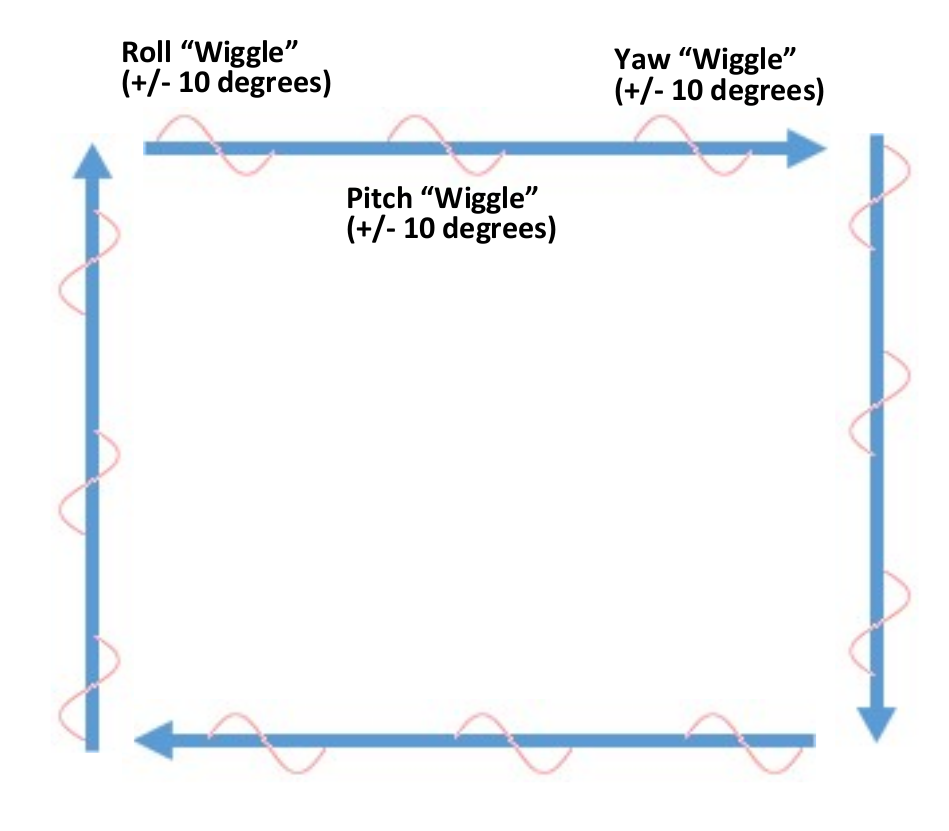
Calibration manuevers - Tolles-Lawson

Fly the aircraft in a series of Roll, Pitch, Yaw maneuvers

• High-altitude

• Altitude of a known map

Maneuver angle should depend upon the expected aircraft dynamics

• Barrel Rolls?

Typically at each cardinal heading

• 3 rolls \(\pm 10^\circ\) at 1 Hz
• 3 pitches \(\pm 10^\circ\) at 1 Hz
• 3 yaws \(\pm 10^\circ\) at 1 Hz

Pack your air-sickness bag

(W. E. Tolles and Lawson 1950), (W. E. Tolles 1954), (W. E. Tolles 1955), (Gnadt, Wollaber, and Nielsen 2022)

Construct Tolles-Lawson \(A\) matrix

\[ A = \begin{bmatrix} \cos X_1 & \cdots & \cos X_N\\ \cos Y_1 & \cdots & \cos Y_N \\ \cos Z_1 & \cdots & \cos Z_N\\ B_\ext \cos^2 X_1 & \cdots & B_\ext \cos^2 X_N\\ B_\ext \cos X_1 \cos Y_1 & \cdots & B_\ext \cos X_N \cos Y_N\\ B_\ext \cos X_1 \cos Z_1 & \cdots & B_\ext \cos X_N \cos Z_N \\ B_\ext \cos^2 Y_1 & \cdots & B_\ext \cos^2 Y_N \\ B_\ext \cos Y_1 \cos Z_1 & \cdots & B_\ext \cos Y_N \cos Z_N\\ B_\ext \cos^2 Z_1 & \cdots & B_\ext \cos^2 Z_N\\ B_\ext \cos X_1 \cos' X_1 & \cdots & B_\ext \cos X_N \cos' X_N \\ B_\ext \cos X_1 \cos' Y_1 & \cdots & B_\ext \cos X_N \cos' Y_N\\ B_\ext \cos X_1 \cos' Z_1 & \cdots & B_\ext \cos X_N \cos' Z_N\\ B_\ext \cos Y_1 \cos' X_1 & \cdots & B_\ext \cos Y_N \cos' X_N\\ \vdots & & \vdots \\ B_\ext \cos Z_1 \cos' Z_1 & \cdots & B_\ext \cos Z_N \cos' Z_N \\ \end{bmatrix} \]

\(B_\ext\) is the magnitude of the external field. We assume that \[ B_\ext = \sqrt{B_x^2 + B_y^2 + B_z^2} \]
Equivalently that the vector mags only see external field. The anomaly signal is below the noise floor.

Solve for the \(c_i\) coefficients

Map-less calibration
Perform maneuvers at fixed frequency \(f\)
Band-pass filter columns of \(A\), \(B_\text{scalar}\) \[ \begin{aligned} A_f & = BPF(A)\\ B_{\text{scalar},f} & = BPF(B_{\text{scalar}}) \end{aligned} \]
Solve for \(c\)

\[ A_f c = B_{\text{scalar},f} \]

Map-based calibration
Perform maneuvers over known-good map

Solve for \(c\)
\[ A c = B_{\text{sensor}} - B_{\earth} - B_{\text{anomaly}} \]

Apply \(c\) to in-flight data for comparison

In-flight
Compute \(A_i\) for each time-step

Apply \(c\)

\[ B_\text{plane} = A c \]
\[ B_\text{anomaly} = B_\text{sensor} - B_\earth - B_\faPlane \]

Gnadt, Albert R., Allan B. Wollaber, and Aaron P. Nielsen. 2022. “Derivation and Extensions of the Tolles-Lawson Model for Aeromagnetic Compensation.” arXiv. https://doi.org/10.48550/ARXIV.2212.09899.

Leliak, Paul. 1961. “Identification and Evaluation of Magnetic-Field Sources of Magnetic Airborne Detector Equipped Aircraft.” IRE Transactions on Aeronautical and Navigational Electronics ANE-8 (3): 95–105. https://doi.org/10.1109/TANE3.1961.4201799.

Tolles, W E, and J D Lawson. 1950. “Magnetic compensation of MAD equipped aircraft.” Airborne Instruments Lab. Inc., Mineola, NY, Rept, 201–1.

Tolles, W. E. 1954. Compensation of aircraft magnetic fields. 2692970, issued 1954.

———. 1955. Magnetic field compensation system. 2706801, issued 1955.