Magnetic Anomaly Navigation Tutorial

IEEE/ION PLANS 2023, Monterey, CA

Aaron Nielsen

The views expressed in this article are those of the author and do not necessarily reflect the official policy or position of the United States Government, Department of Defense, United States Air Force or Air University.

Distribution A: Authorized for public release. Distribution is unlimited. Case No. 2023-0277.

Magnetic Anomaly Navigation Tutorial

  • Overview of Magnetic Anomaly Navigation
  • Tutorial goals:
    • Calibrate and Navigate an aircraft

Outline

Schedule

Tutorial is 90 minutes total:

  • 40 minutes
  • 10 minutes break
  • 40 minutes

Outline

Magnetic Anomaly Navigation Overview

Requirements for MagNav

Discuss publicly available MagNav software and dataset

Learn and perform traditional aircraft calibration
- Tolles-Lawson

Evaluate navigation performance

Calibration/noise removal

Navigation performance improvement

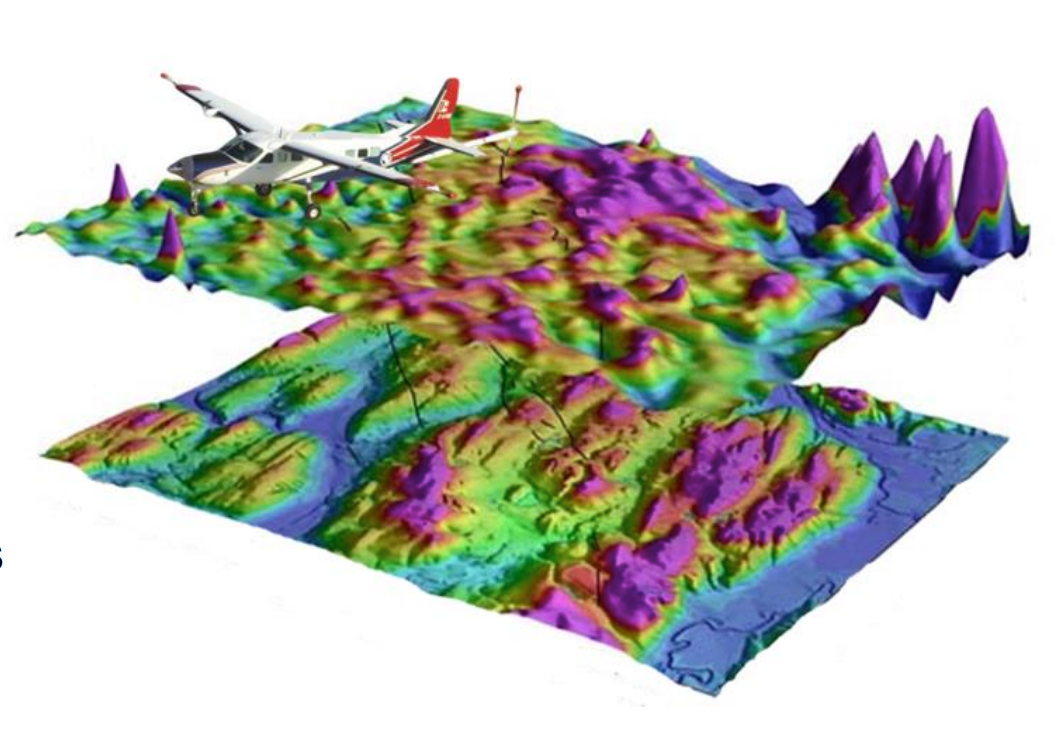
MagNav Overview

Magnetic Anomaly Navigation Overview

Refrigerator magnet

Earth’s core field (compass)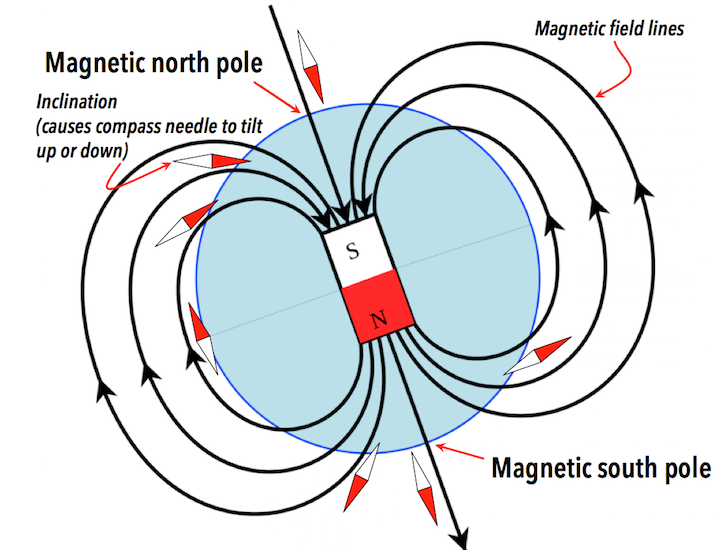

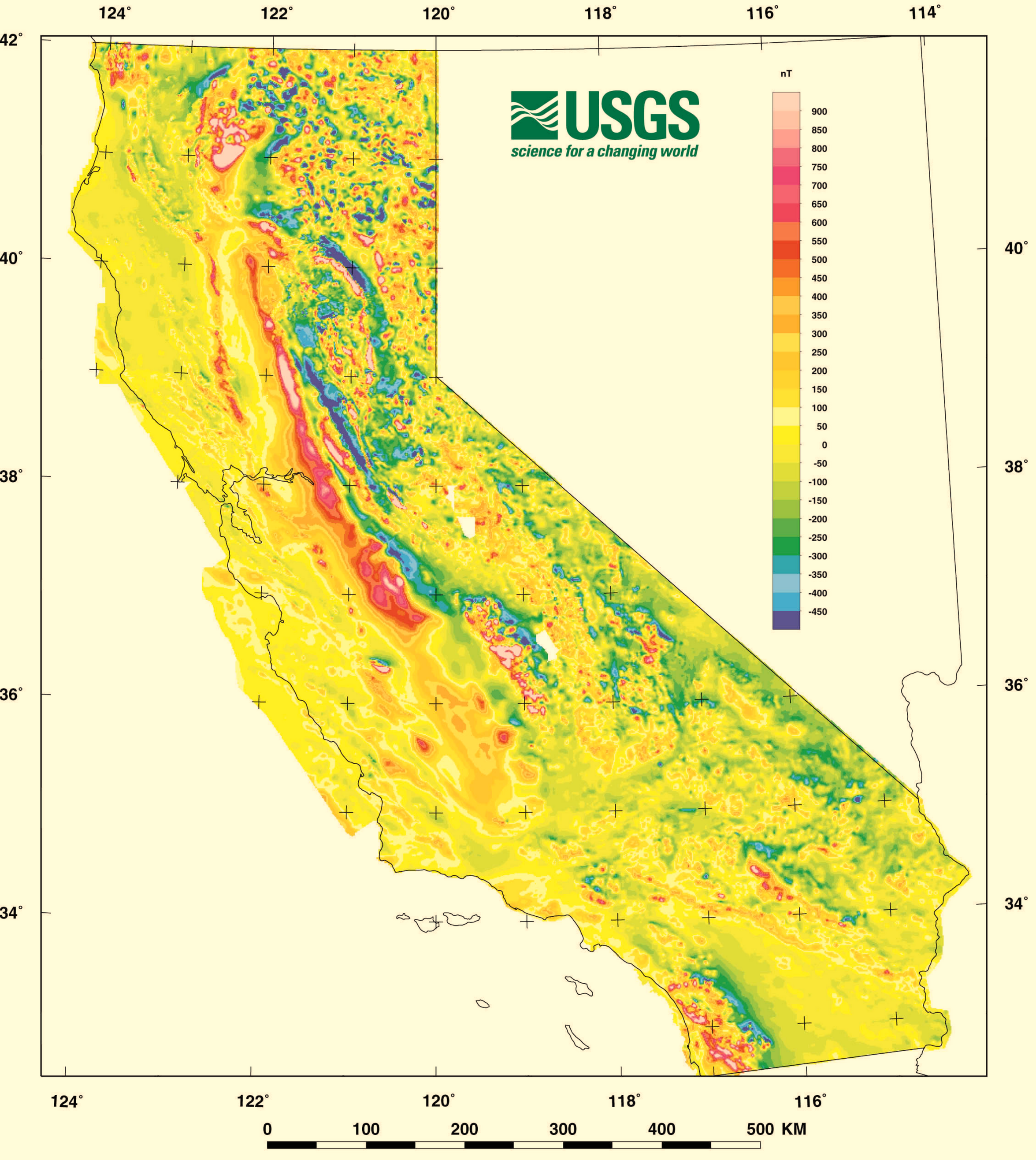
Crustal magnetic anomaly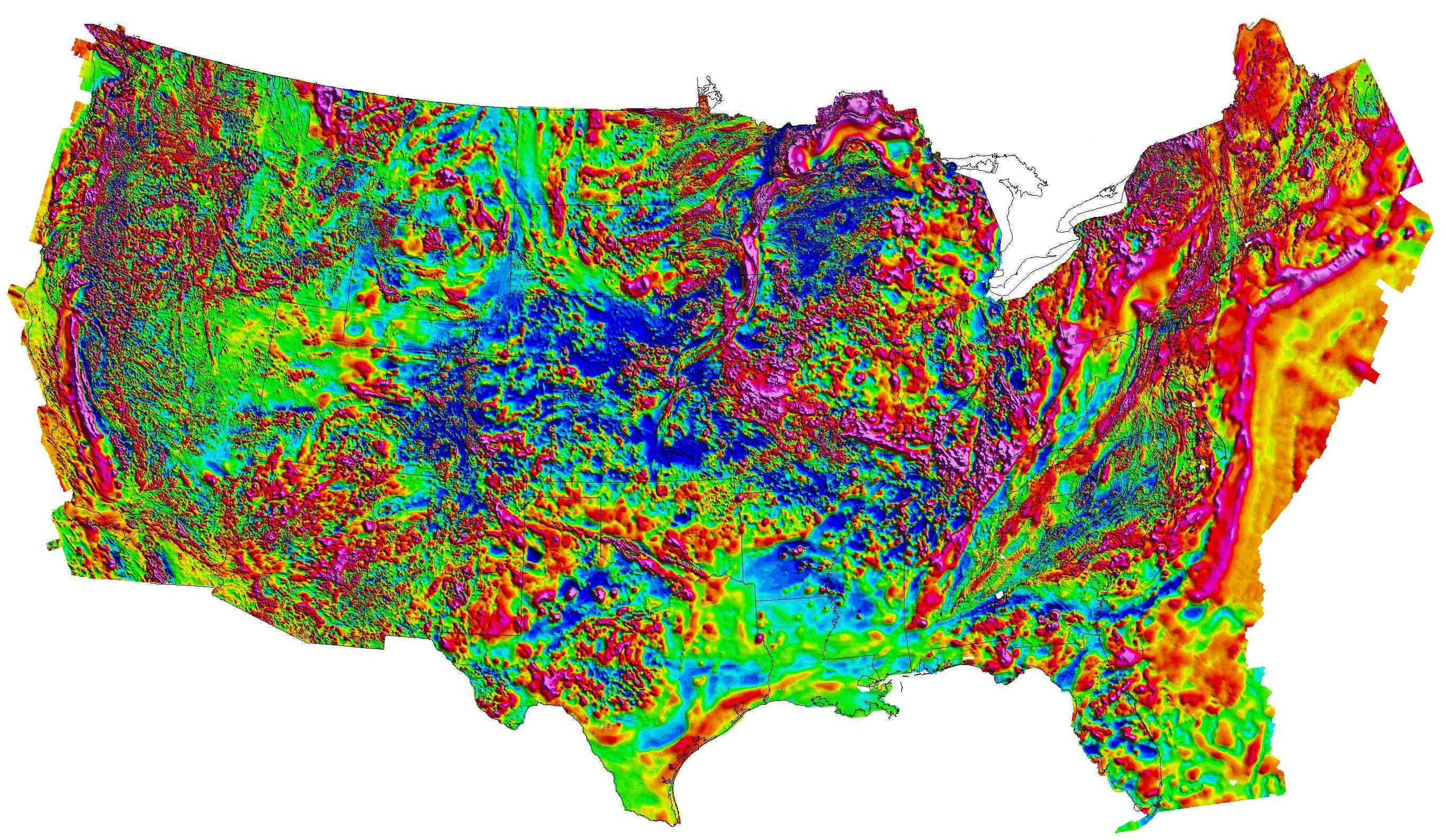

1 000 000 nT

50 000 nT https://www.ncei.noaa.gov/products/world-magnetic-model (Chulliat 2020)

Range \(\pm\) 500 nT
Resolution \(\sim\) 1 nT https://mrdata.usgs.gov/magnetic/ (Bankey et al. 2002)

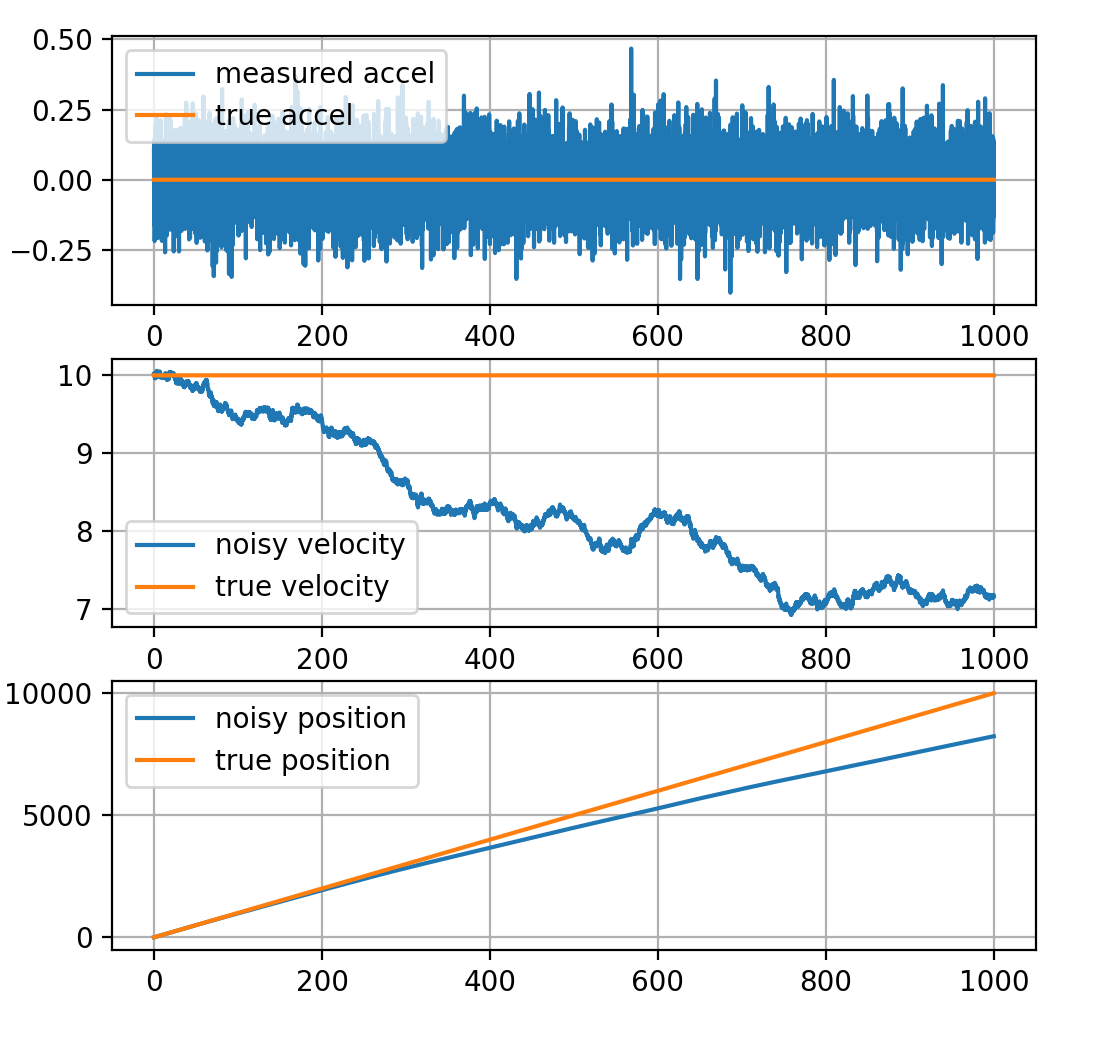
Inertial Navigation

Inertial Measurement Unit (IMU)

  • measures accelerations
  • measures rotation rates

To get position from accleration, you have to integrate twice

  • continuously adds noise to your position estimate

Drifting position estimate needs to be corrected

  • Magnetic Anomaly Navigation matches to magnetic anomaly map

Earth Magnetic Anomaly Grid 2-arcsec v3

(Meyer, Chulliat, and Saltus 2017)

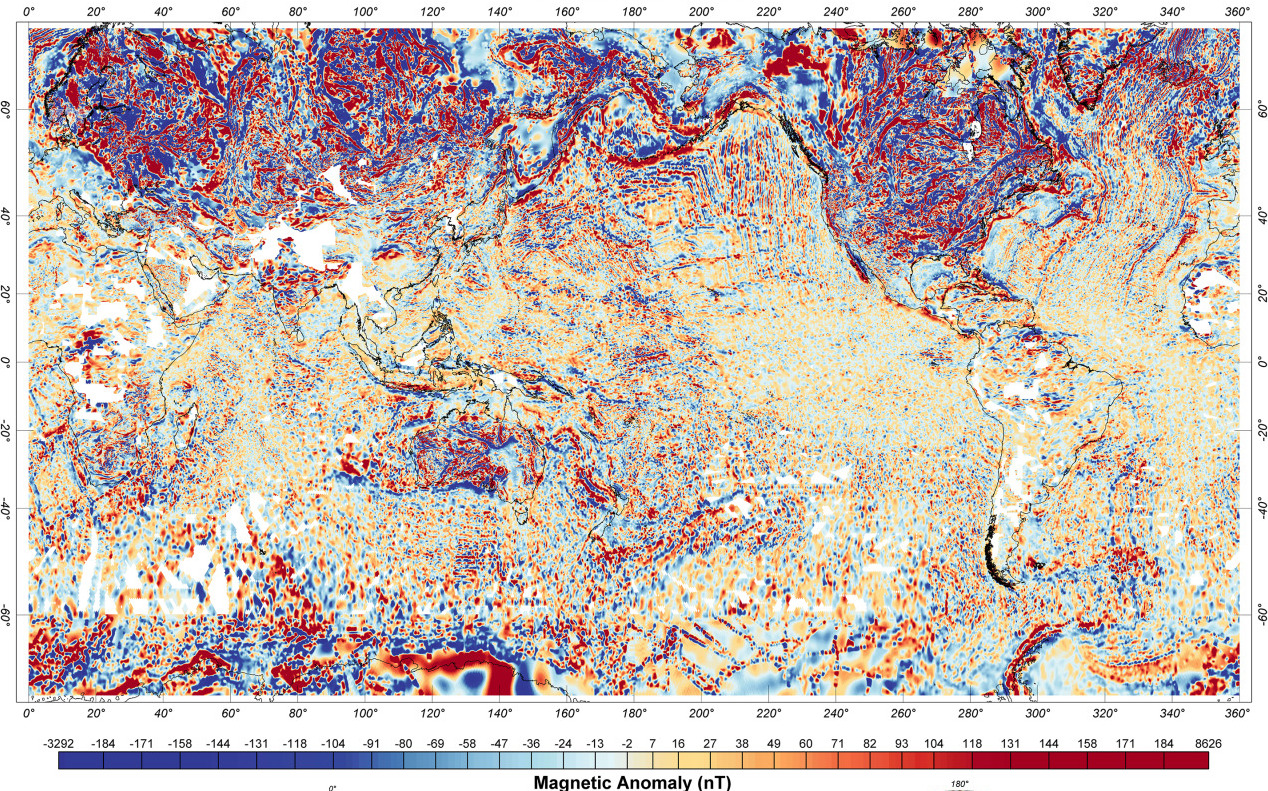
Map-based navigation

Features are required to navigate

Magnetic anomaly closely tied to geology

  • less variation in coastal region
  • direction variation in Central Valley
  • more structure in Sierra Nevada mountains

Area and direction of travel make a difference

(Roberts and Jachens 2000)

Interpretation of magnetic anomaly

-The primary sensor used is a scalar magnetometer which measures: \(|\vec{B}|\)

-The field is a vector \(\vec{B}\)

-Interpretation of \(|\vec{B}|\) relies on understanding
\(|\vec{B}_\sensor| = |\vec{B}_\earth + \vec{B}_\text{anomaly}|\)

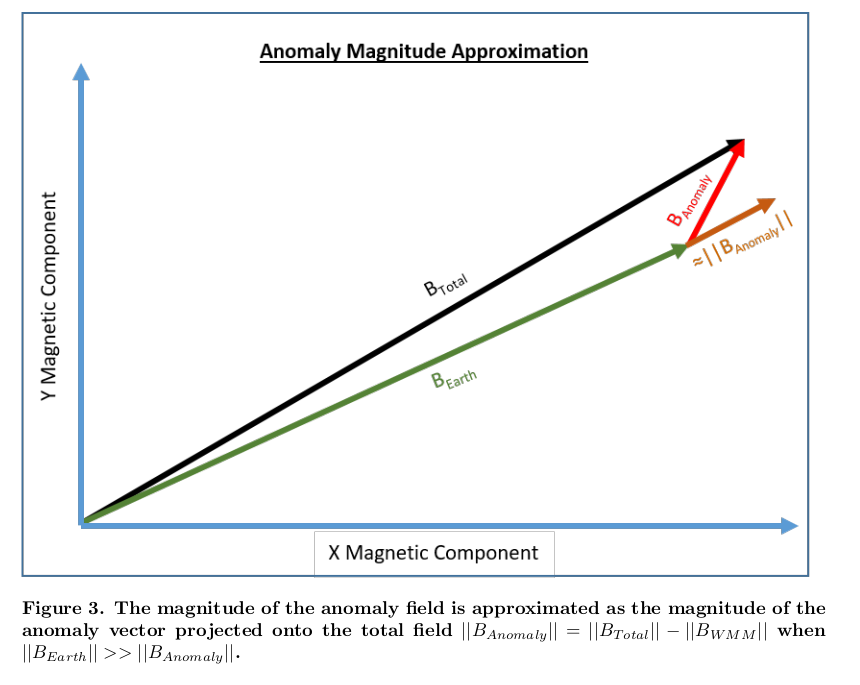
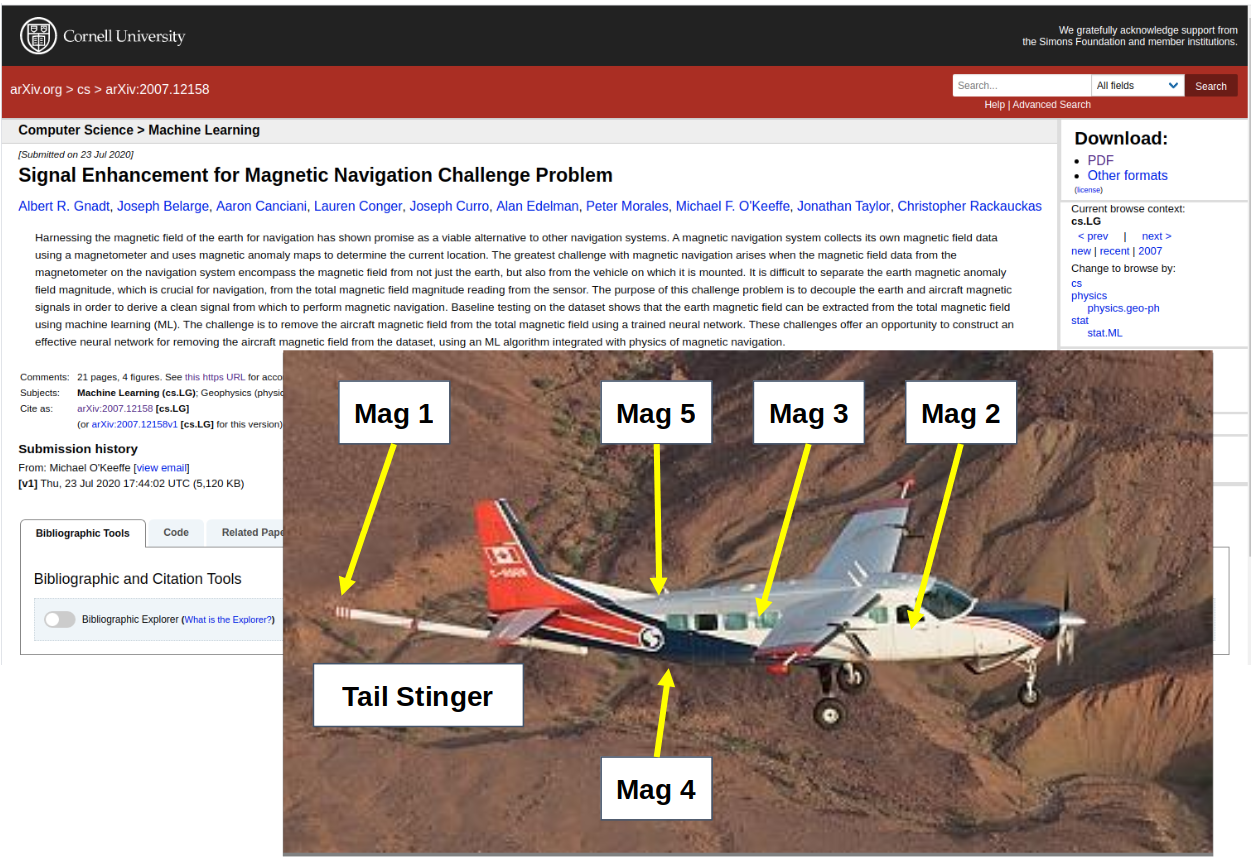
An airplane is a big magnet that flies

\(|\vec{B}| = |\vec{B}_\earth + \vec{B}_\text{anomaly} + \vec{B}_\plane|\)

Aircraft Calibration

Sensor placement and installation

  • Engineered location
    • Stinger
  • Survey for placement
  • Non-magnetic fasteners

Degaussing

Algorithms

Sander Geophysics, Ltd

xkcd

CC BY-NC 2.5

Software and Data for Tutorial

MIT-AF AI Accelerator MagNav project

https://arxiv.org/abs/2007.12158, (Gnadt et al. 2020)

It can be simple as:

docker run -p 8888:8888 jtaylormit/magnav

Data run-thru

  • Collected data made publicly available:
  • Recorded flight data near Ottawa, ON
    • Position, velocity, attitude (truth)
    • Tail Stinger
    • 4 magnetometers in cabin
    • Current and voltage sensors
    • 10 Hz
  • Ground station reference sensor
    • 10 Hz
  • Magnetic Maps of flight area
  • Calibration maneuvers
  • Flight crew notes
    • Power lines
    • Railroad tracks
  • On-board activities
    • power on/off to systems
    • movement of iron bars
  • Professional calibration results

MagNav Software - MagNav.jl

https://github.com/MIT-AI-Accelerator/MagNav.jl

MagNav.jl Documentation

https://mit-ai-accelerator.github.io/MagNav.jl/stable/

MagNav.jl Docker image

https://hub.docker.com/r/jtaylormit/magnav

Challenge problem

https://magnav.mit.edu

Julia Language

https://julialang.org

Get MagNav.jl and use it

using Pkg
Pkg.add(url="https://github.com/MIT-AI-Accelerator/MagNav.jl", version="0.4.1")

Maps

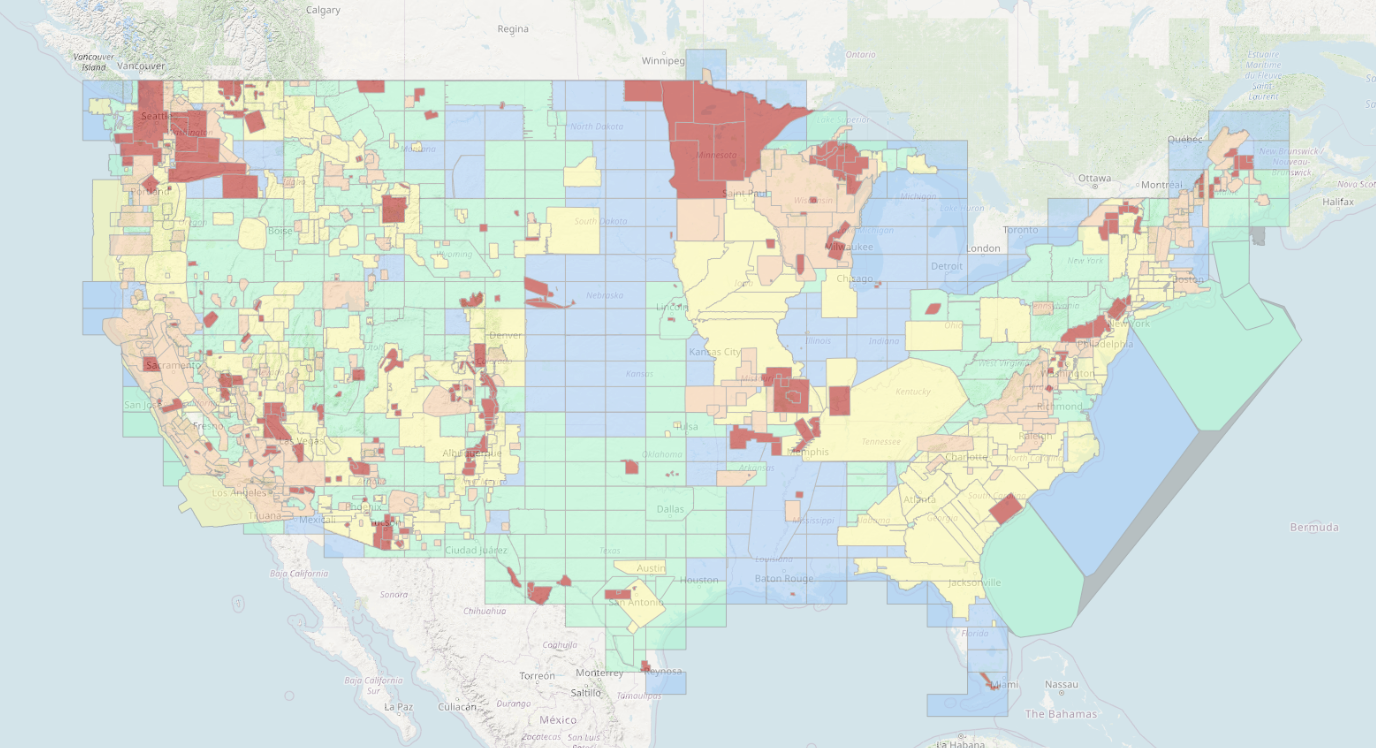
Airborne magnetic anomaly surveys

  • Usually performed in smaller area for geological interpretation
  • Large anomaly maps merged together in mosaic using a leveling process
    • Meant to merge long spatial wavelengths
  • Many anomaly surveys pre-date GPS
    • Geolocated via air-crew observations
  • Typically remove space-weather effects with ground-station

USGS Magnetic Data

https://mrdata.usgs.gov/airborne/map-us.html

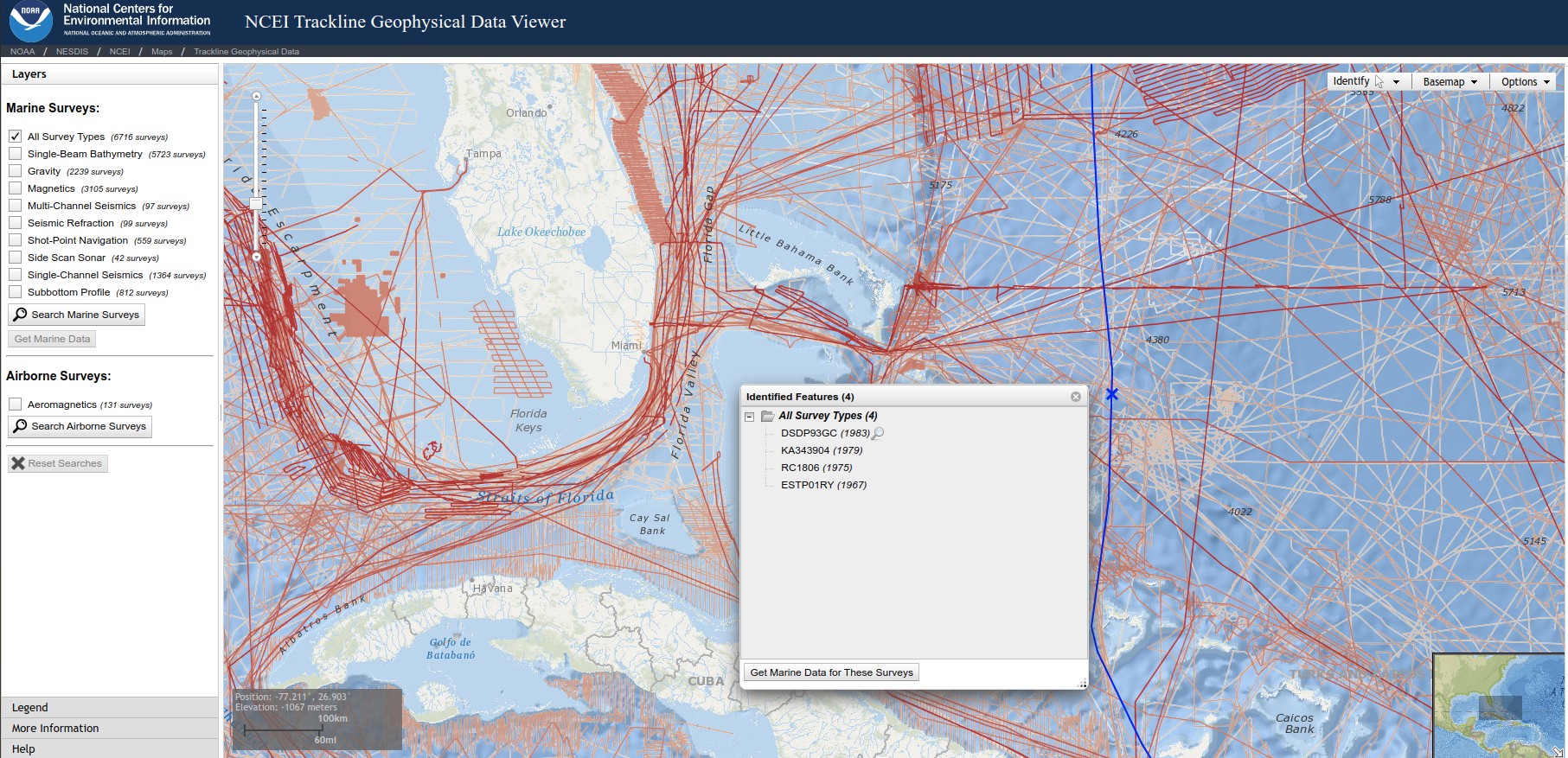
Marine track surveys

  • Often single long track following ship
  • Many pre-date GPS
    • Use ship’s positioning
  • Typically no space weather correction

NCEI NOAA Trackline database

https://www.ncei.noaa.gov/maps/geophysics/

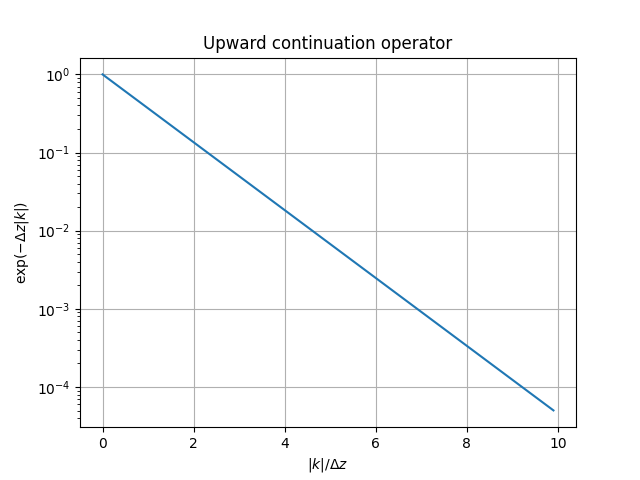
Upward continuation

Magnetic anomaly maps are usually made at a single altitude.

The process of taking a magnetic map from one altitude to another.

  • \(F(B_\text{up}) = F(B_\text{known}) e^{-\Delta z |k|}\)
  • Assumes a flat Earth model with all the sources below
  • (Blakely 1995)

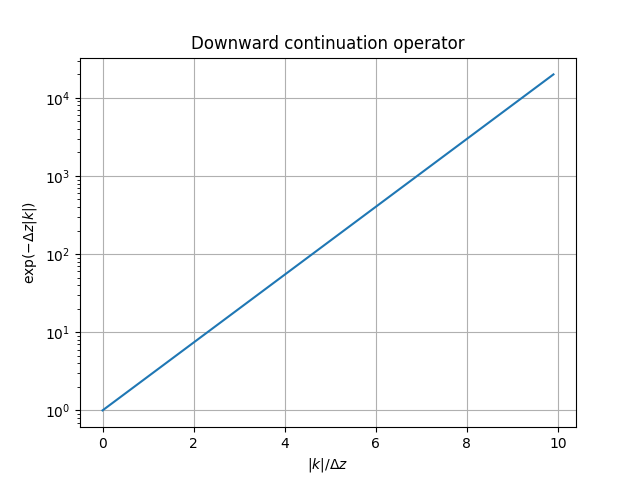
Dangerous downward continuation

The process of taking a magnetic map from one altitude to another.

  • \(F(B_\text{down}) = F(B_\text{known}) e^{+\Delta z |k|}\)
  • Noise can be amplified
  • Techniques to do this exist, and involve some kind of regularization or source estimation
  • (Blakely 1995)

Calibration

Tolles-Lawson

  • Calibration technique developed in WW2 for submarine hunting
  • Declassified in 1950’s and patented
  • Standard calibration technique used for aero-magnetic surveys

\[ \begin{align*} |B_\mathrm{Sensor}| &= |\vec{B}_\ext + \vec{B}_\faPlane|\\ &= \sqrt{ |B_\ext|^2 + |B_\faPlane|^2 + 2 |B_\ext||B_\faPlane|\cos\theta}\\ |B_\text{Sensor}| &= |B_\ext| \sqrt{ 1 + \frac{|B_\faPlane|^2}{|B_\ext|^2} + 2\frac{|B_\faPlane|}{|B_\ext|}\cos\theta} \end{align*} \]

Tolles-Lawson Path to Calibration 1/2

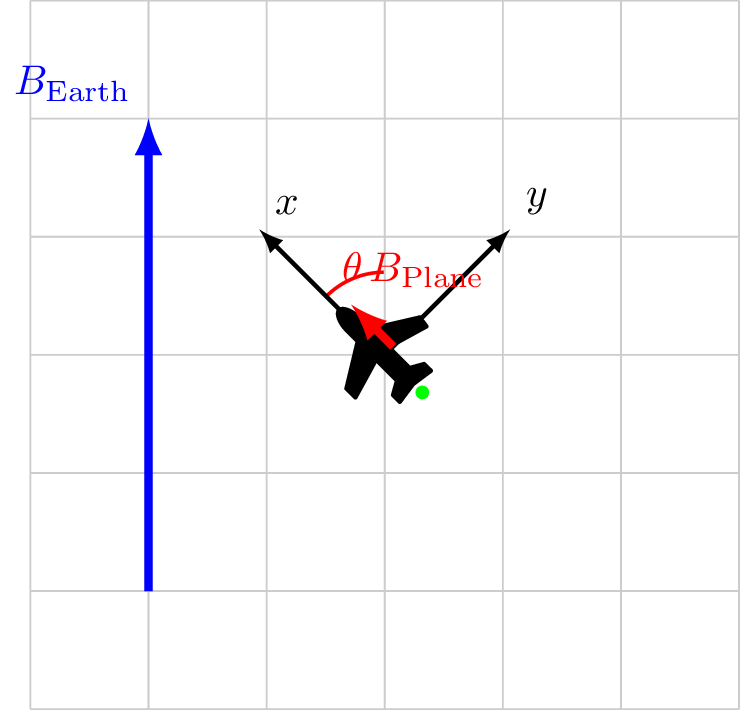
\[ \begin{align*} |B_\text{Sensor}| &= |\vec{B}_\ext + \vec{B}_\faPlane|\\ &= \sqrt{ |B_\ext|^2 + |B_\faPlane|^2 + 2 |B_\ext||B_\faPlane|\cos\theta}\\ |B_\text{Sensor}| &= |B_\ext| \sqrt{ 1 + 2\frac{|B_\faPlane|}{|B_\ext|}\cos\theta}\\ &\approx |B_\ext| + |B_\faPlane|\cos\theta + \cdots \end{align*} \]

Path to Calibration
Measure \(\cos\theta\)

Solve \(|B_\text{sensor}| = |B_\ext| + |B_\plane|\cos\theta\)

Assuming \(|B_\ext|\) is known or constant

Tolles-Lawson Path to Calibration 2/2

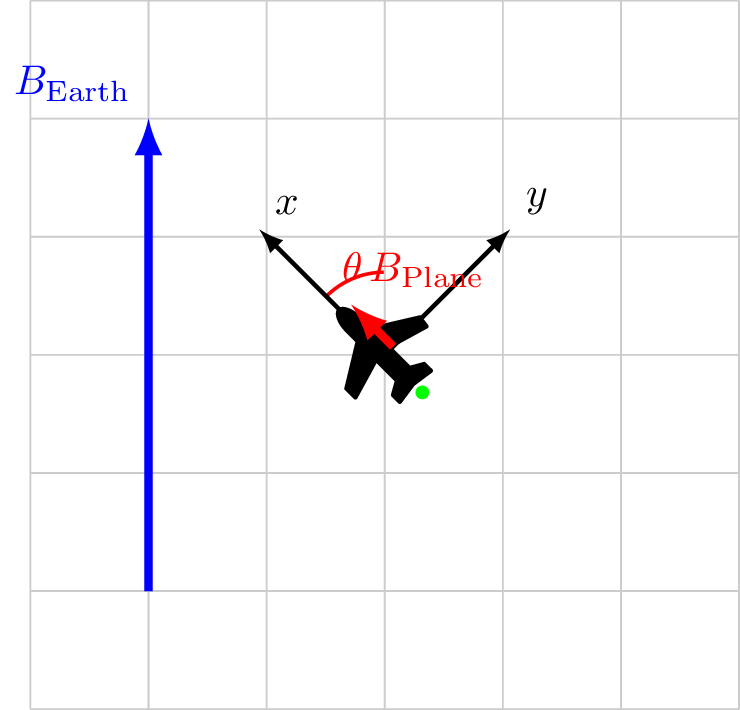
Path to Calibration
Measure \(\cos\theta\)

Solve \(|B_\text{sensor}| = |B_\ext| + |B_\faPlane|\cos\theta\)

Assuming \(|B_\ext|\) is known or constant


How to measure \(\cos\theta\)?
Use a vector magnetometer

Rotate aircraft in \(|B_\ext|\)

Compute direction cosines…

Direction cosines

  • The direction cosines are computed in the vector magnetometer reference frame
  • The magnetometer is fixed to aircraft body reference frame \[ \begin{aligned} \cos X = & \frac{B_x}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Y = & \frac{B_y}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Z = & \frac{B_z}{\sqrt{B_x^2 + B_y^2 + B_z^2}} \end{aligned} \]

In the 2-D example, \(B_z = 0\)

Calibration 1/4

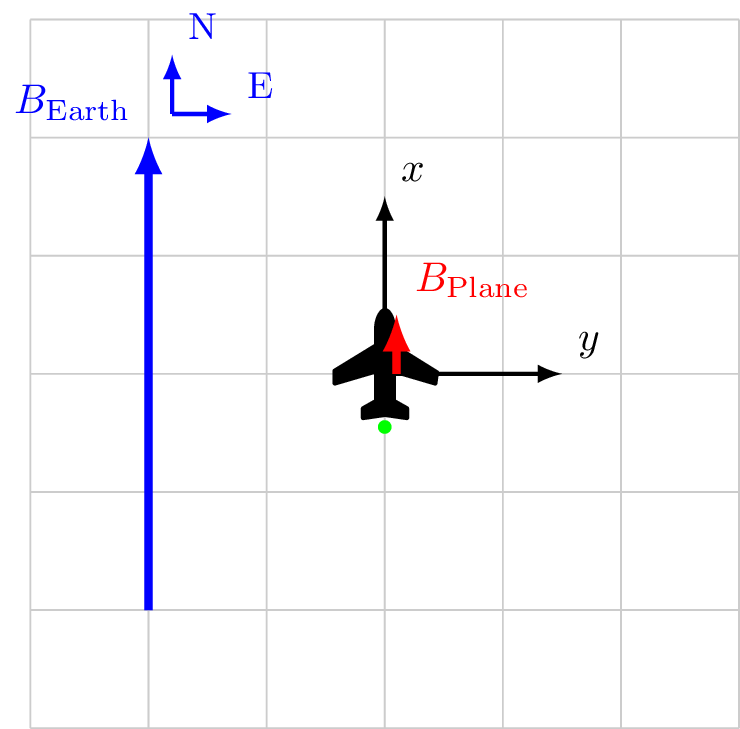
Coordinate system fixed to aircraft
\[\vec{B}_\mathrm{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= 4.0 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && +0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= 4.5 \hat{x} && + 0.0 \hat{y} \\ |B_\text{Sensor}| &= 4.5 && \\ \cos X &= \frac{4.5}{4.5} && = 1\\ \cos Y &= \frac{0.0}{4.5} && = 0\\ \end{alignat*} \]

Calibration 2/4

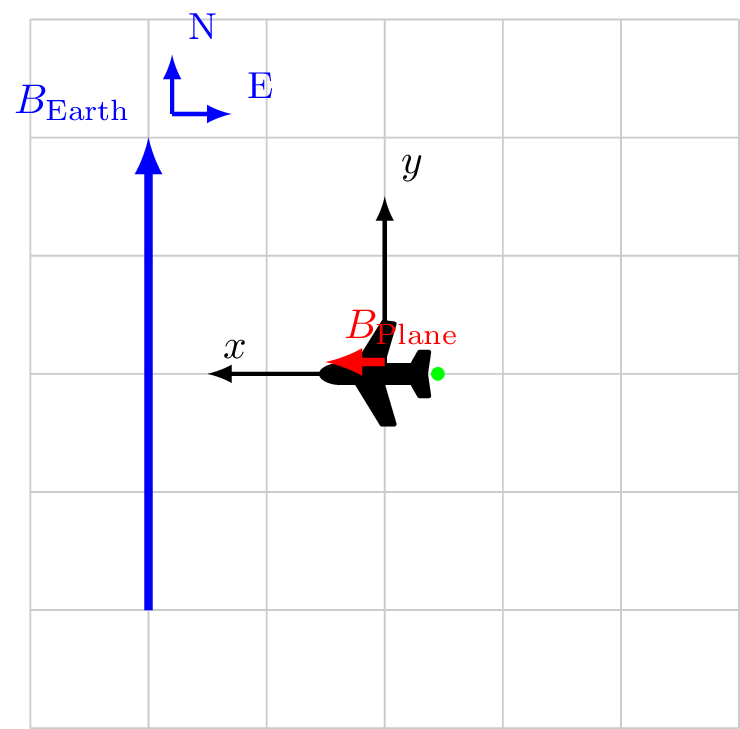
Coordinate system fixed to aircraft
\[\vec{B}_\text{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= 0.0 \hat{x} && + 4.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= 0.5 \hat{x} && + 4.0 \hat{y} \\ |B_\text{Sensor}| &= 4.007 && \\ \cos X &= \frac{0.5}{4.007} && \ne 0 \rightarrow 82.8^\circ\\ \cos Y &= \frac{4.0}{4.007} && \approx 1\\ \end{alignat*} \]

Calibration 3/4

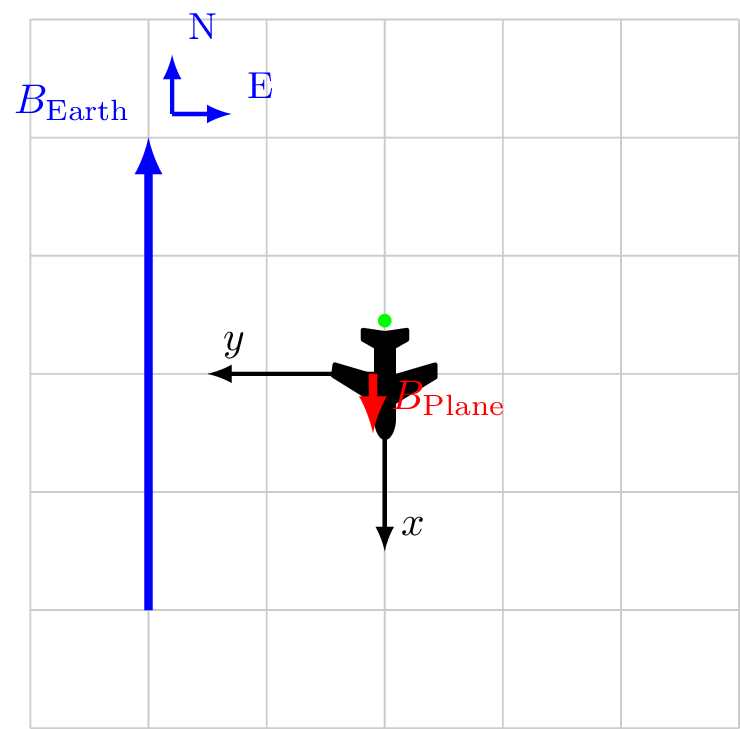
Coordinate system fixed to aircraft
\[\vec{B}_\text{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= -4.0 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= -3.5 \hat{x} && + 0.0 \hat{y} \\ |B_\text{Sensor}| &= 3.5 && \\ \cos X &= \frac{-3.5}{3.5} && = -1\\ \cos Y &= \frac{0}{3.5} && = 0\\ \end{alignat*} \]

Calibration 4/4

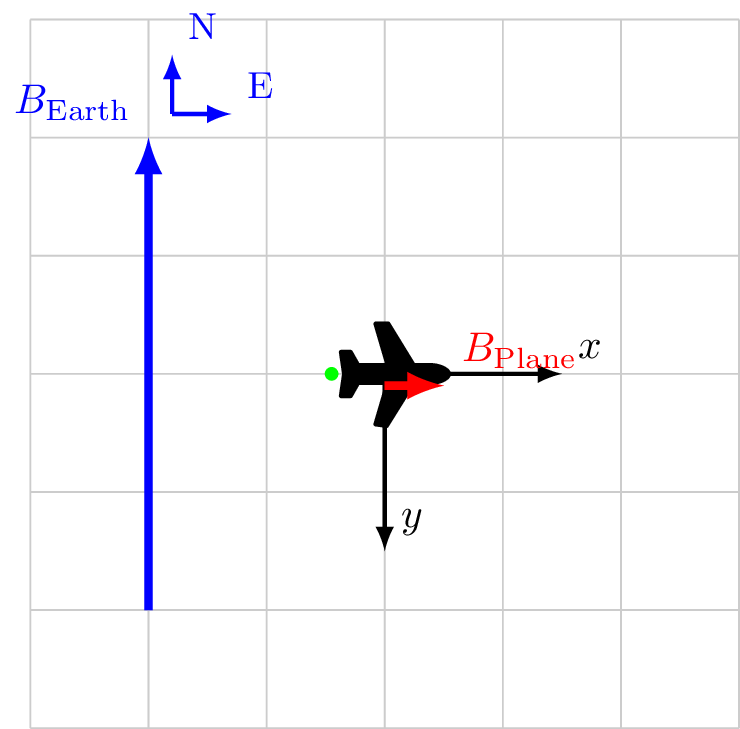
Coordinate system fixed to aircraft
\[\vec{B}_\text{Sensor} = \vec{B}_\ext + \vec{B}_\faPlane\]
\[ \begin{alignat*}{3} \vec{B}_\ext &= 0.0 \hat{x} && + -4.0 \hat{y} \\ \vec{B}_\faPlane &= 0.5 \hat{x} && + 0.0 \hat{y} \\ \vec{B}_\text{Sensor} &= 0.5 \hat{x} && + -4.0 \hat{y} \\ |B_\text{Sensor}| &= 4.007 &&\\ \cos X &= \frac{0.5}{4.007} && \ne 0\\ \cos Y &= \frac{-4.0}{4.007} && \approx -1\\ \end{alignat*} \]

Standard calibration model

\[|\vec{B}| = |\vec{B}_\ext + \vec{B}_\faPlane|\]

\[ \begin{array}{ l B c B c B c } \vec{B}_\faPlane & = & \vec{B}_\text{Permanent} & + & \vec{B}_\text{Induced} & + & \vec{B}_\text{Eddy}\\ & = & \vec{P}_\text{constant} {} & + &{} M_{3\times3} \vec{B }_\ext {} & + & {} S_{3\times3} \frac{\partial}{\partial t} \vec{B}_\ext \end{array} \]

\(M_{3\times3}\) is symmetric \(\rightarrow\) 6 independent elements

Total of 18 elements

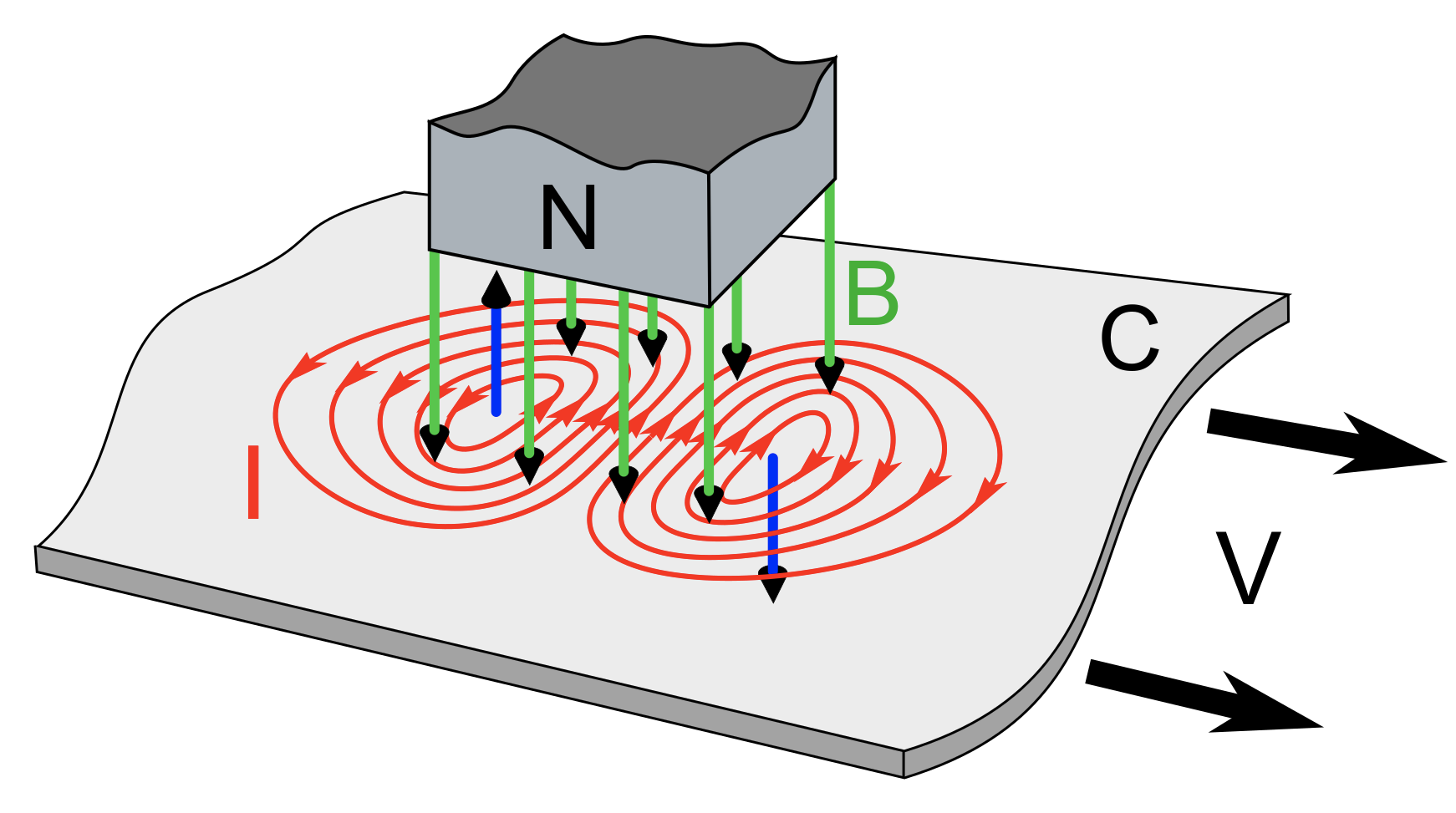
Use the same direction cosines, now with \(B_z\)

The direction cosines are computed from the vector magnetometer

\[ \begin{aligned} \cos X = & \frac{B_x}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Y = & \frac{B_y}{\sqrt{B_x^2 + B_y^2 + B_z^2}}\\ \cos Z = & \frac{B_z}{\sqrt{B_x^2 + B_y^2 + B_z^2}} \end{aligned} \]

Tolles-Lawson full implementation

\[ \begin{aligned} B_\plane & = & & { c_1 \cos X + c_2 \cos Y + c_3 \cos Z }+ \\ & & B_\ext & {[ c_4 \cos^2 X + c_5 \cos X \cos Y + c_6 \cos X \cos Z +} \\ & & & { c_7 \cos^2 Y + c_8 \cos Y \cos Z + c_9 \cos^2 Z ] + } \\ & & B_\ext & { [ c_{10} \cos X \cos' X + c_{11} \cos X \cos' Y + c_{12} \cos X \cos' Z }+ \\ & & & { c_{13} \cos Y \cos' X + c_{14} \cos Y \cos' Y + c_{15} \cos Y \cos' Z +} \\ & & & { c_{16} \cos Z \cos' X + c_{17} \cos Z \cos' Y + c_{18} \cos Z \cos' Z ] } \end{aligned} \]

We need a method to solve for \(c_1 \ldots c_{18}\)

How to sample the range of possible angles?

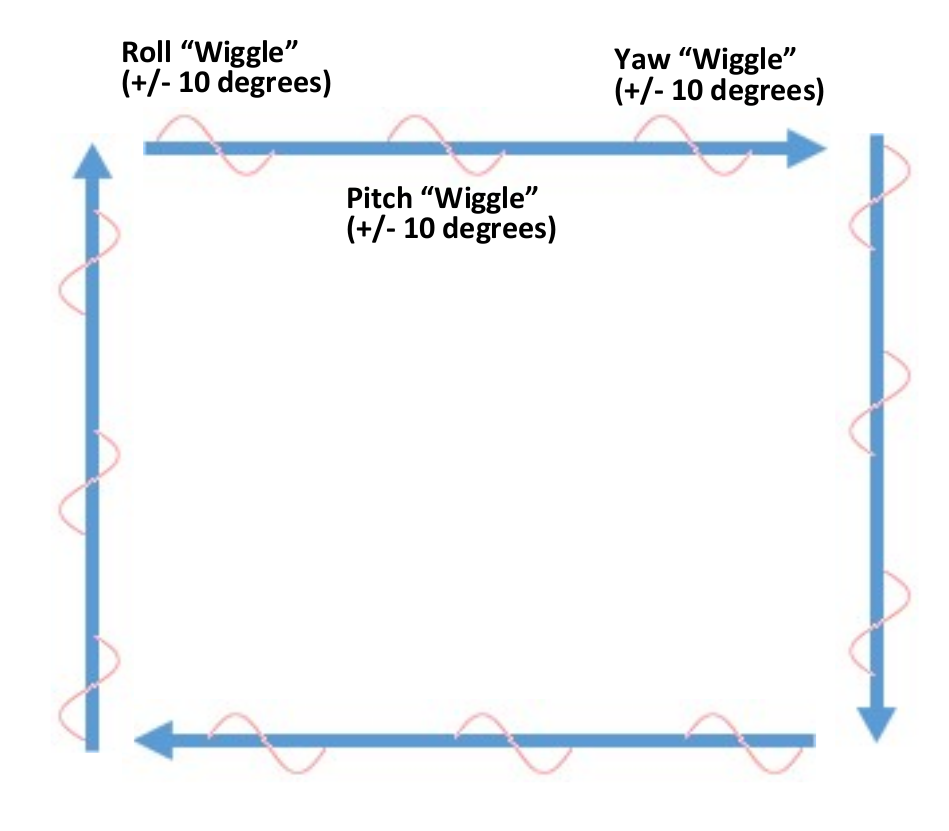
Calibration manuevers - Tolles-Lawson

Fly the aircraft in a series of Roll, Pitch, Yaw maneuvers

  • High-altitude

  • Altitude of a known map

Maneuver angle should depend upon the expected aircraft dynamics

  • Barrel Rolls?

Typically at each cardinal heading

  • 3 rolls \(\pm 10^\circ\) at 1 Hz
  • 3 pitches \(\pm 10^\circ\) at 1 Hz
  • 3 yaws \(\pm 10^\circ\) at 1 Hz

Pack your air-sickness bag

(W. E. Tolles and Lawson 1950), (W. E. Tolles 1954), (W. E. Tolles 1955), (Gnadt, Wollaber, and Nielsen 2022)

Construct Tolles-Lawson \(A\) matrix

\[ A = \begin{bmatrix} \cos X_1 & \cdots & \cos X_N\\ \cos Y_1 & \cdots & \cos Y_N \\ \cos Z_1 & \cdots & \cos Z_N\\ B_\ext \cos^2 X_1 & \cdots & B_\ext \cos^2 X_N\\ B_\ext \cos X_1 \cos Y_1 & \cdots & B_\ext \cos X_N \cos Y_N\\ B_\ext \cos X_1 \cos Z_1 & \cdots & B_\ext \cos X_N \cos Z_N \\ B_\ext \cos^2 Y_1 & \cdots & B_\ext \cos^2 Y_N \\ B_\ext \cos Y_1 \cos Z_1 & \cdots & B_\ext \cos Y_N \cos Z_N\\ B_\ext \cos^2 Z_1 & \cdots & B_\ext \cos^2 Z_N\\ B_\ext \cos X_1 \cos' X_1 & \cdots & B_\ext \cos X_N \cos' X_N \\ B_\ext \cos X_1 \cos' Y_1 & \cdots & B_\ext \cos X_N \cos' Y_N\\ B_\ext \cos X_1 \cos' Z_1 & \cdots & B_\ext \cos X_N \cos' Z_N\\ B_\ext \cos Y_1 \cos' X_1 & \cdots & B_\ext \cos Y_N \cos' X_N\\ \vdots & & \vdots \\ B_\ext \cos Z_1 \cos' Z_1 & \cdots & B_\ext \cos Z_N \cos' Z_N \\ \end{bmatrix} \]

\(B_\ext\) is the magnitude of the external field. We assume that \[ B_\ext = \sqrt{B_x^2 + B_y^2 + B_z^2} \]
Equivalently that the vector mags only see external field. The anomaly signal is below the noise floor.

Solve for the \(c_i\) coefficients

Map-less calibration
Perform maneuvers at fixed frequency \(f\)
Band-pass filter columns of \(A\), \(B_\text{scalar}\) \[ \begin{aligned} A_f & = BPF(A)\\ B_{\text{scalar},f} & = BPF(B_{\text{scalar}}) \end{aligned} \]
Solve for \(c\)

\[ A_f c = B_{\text{scalar},f} \]

Map-based calibration
Perform maneuvers over known-good map

Solve for \(c\)
\[ A c = B_{\text{sensor}} - B_{\earth} - B_{\text{anomaly}} \]

Apply \(c\) to in-flight data for comparison

In-flight
Compute \(A_i\) for each time-step

Apply \(c\)

\[ B_\text{plane} = A c \]
\[ B_\text{anomaly} = B_\text{sensor} - B_\earth - B_\faPlane \]

MagNav.jl example setup

Load the data which includes the following dataframes:

Dataframe Description
df_map Map files for SGL flights
df_comp SGL compensation flight lines
df_flight SGL flight files
df_all All flight lines
df_nav All navigation capable flight lines
df_events Pilot-recorded flight events
Code 
include("common_setup.jl");

Find flight with Tolles-Lawson maneuvers

Dataframe df_comp has flight times of compensation maneuvers

Code 
print(df_comp)
16×5 DataFrame
 Row │ flight   line     t_start  t_end    map_name    
     │ Symbol   Float64  Float64  Float64  Symbol?     
─────┼─────────────────────────────────────────────────
   1 │ Flt1002  1002.02  46390.9  46964.5  missing     
   2 │ Flt1002  1002.02  47027.1  47546.3  missing     
   3 │ Flt1002  1002.2   66571.7  67131.8  missing     
   4 │ Flt1002  1002.2   67276.8  67839.2  missing     
   5 │ Flt1006  1006.02  47222.0  48213.0  missing     
   6 │ Flt1006  1006.04  49165.3  49798.5  missing     
   7 │ Flt1006  1006.04  49940.1  50318.5  missing     
   8 │ Flt1006  1006.04  50340.7  50804.2  missing     
   9 │ Flt1006  1006.04  50829.7  51301.7  missing     
  10 │ Flt1006  1006.04  51377.5  52013.8  missing     
  11 │ Flt1006  1006.04  52013.8  52372.0  missing     
  12 │ Flt1006  1006.04  52408.4  52843.1  missing     
  13 │ Flt1006  1006.04  52861.8  53286.0  missing     
  14 │ Flt1006  1006.06  53855.0  54510.0  missing     
  15 │ Flt1006  1006.08  55774.5  56192.0  Eastern_395
  16 │ Flt1006  1006.08  56192.0  56609.0  Eastern_395

Select Flight 1006 for analysis:

Code 
flight   = :Flt1006 # specify flight, full list of SGL flights is in df_flight
xyz      = get_XYZ(flight,df_flight); # load all flight data
traj_flt = get_traj(xyz); # load truth trajectory for flight

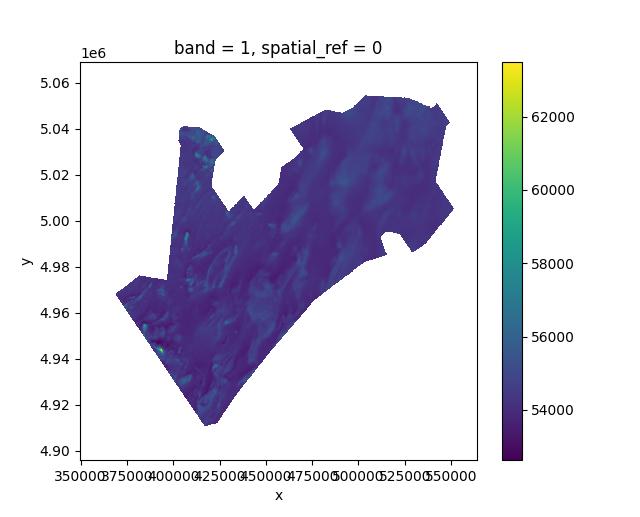
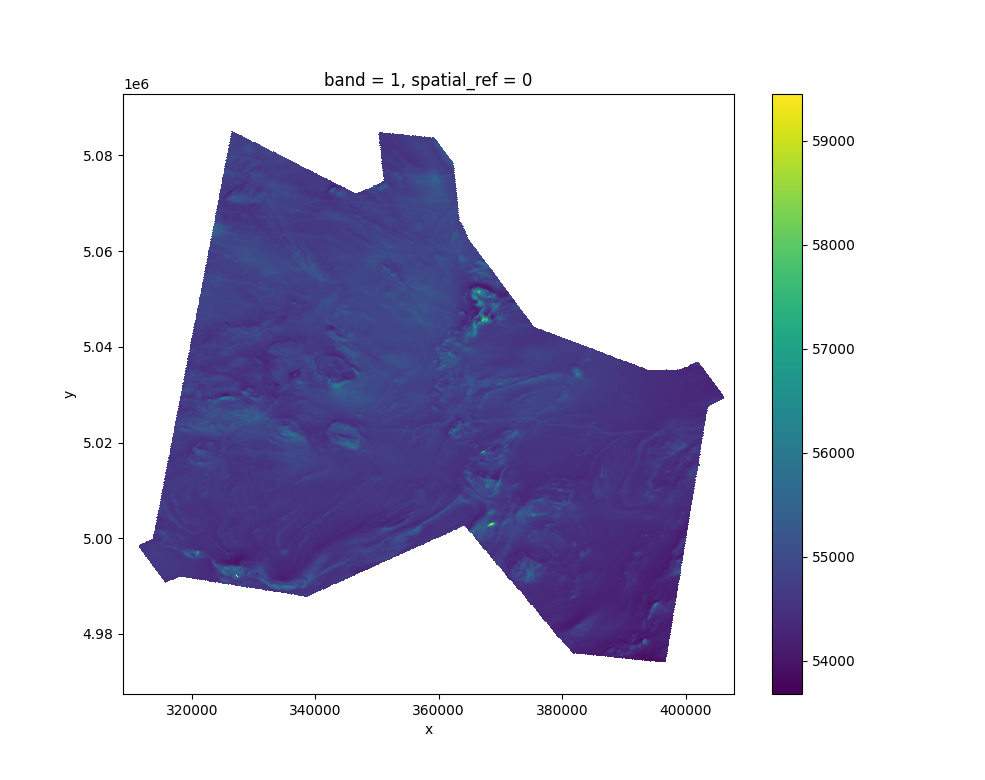
Load a magnetic anomaly map and plot it

Code 
map_name   = :Eastern_plot;
mapS = get_map(map_name,df_map); # load map data
p3 = plot_map(mapS;legend=false) # plot map
plot(p3; single_pane_defs...)

Plot the GPS flight trajectory with map

Code 
p3 = plot_map(mapS;legend=false); # plot map 
plot_path!(p3,traj_flt;path_color=:black);
plot(p3; double_pane_defs...);

Code 
palt = plot(
     traj_flt.tt,
     traj_flt.alt,
     xlabel="Time(seconds)",
     ylabel="Altitude(meters)",
     legend=false,
     linecolor=:black)
plot(palt; double_pane_defs...)

Select data for Tolles-Lawson calibration

Code 
print(df_comp) # df_comp describes compensation maneuvers
TL_i   = 6; # select first calibration box of 1006.04
TL_ind = get_ind(xyz;tt_lim=[df_comp.t_start[TL_i],df_comp.t_end[TL_i]]); # get indices
16×5 DataFrame
 Row │ flight   line     t_start  t_end    map_name    
     │ Symbol   Float64  Float64  Float64  Symbol?     
─────┼─────────────────────────────────────────────────
   1 │ Flt1002  1002.02  46390.9  46964.5  missing     
   2 │ Flt1002  1002.02  47027.1  47546.3  missing     
   3 │ Flt1002  1002.2   66571.7  67131.8  missing     
   4 │ Flt1002  1002.2   67276.8  67839.2  missing     
   5 │ Flt1006  1006.02  47222.0  48213.0  missing     
   6 │ Flt1006  1006.04  49165.3  49798.5  missing     
   7 │ Flt1006  1006.04  49940.1  50318.5  missing     
   8 │ Flt1006  1006.04  50340.7  50804.2  missing     
   9 │ Flt1006  1006.04  50829.7  51301.7  missing     
  10 │ Flt1006  1006.04  51377.5  52013.8  missing     
  11 │ Flt1006  1006.04  52013.8  52372.0  missing     
  12 │ Flt1006  1006.04  52408.4  52843.1  missing     
  13 │ Flt1006  1006.04  52861.8  53286.0  missing     
  14 │ Flt1006  1006.06  53855.0  54510.0  missing     
  15 │ Flt1006  1006.08  55774.5  56192.0  Eastern_395
  16 │ Flt1006  1006.08  56192.0  56609.0  Eastern_395

Plot calibration trajectory data

Code 
p3 = plot_map(mapS;legend=false); # plot map 
plot_path!(p3,traj_flt,TL_ind;path_color=:black);
plot(p3; double_pane_defs...);

Code 
palt = plot(
     traj_flt.tt[TL_ind],
     traj_flt.alt[TL_ind],
     xlabel="Time(seconds)",
     ylabel="Altitude(meters)",
     legend=false,
     linecolor=:black)
plot(palt; double_pane_defs...)

How good is the professional calibration?

Code 
use_mags = [:mag_1_c, :mag_1_uc];
p = plot_mag(xyz; ind=TL_ind, use_mags = use_mags);
plot(p; single_pane_defs...);

Tail stinger:
- mag_1_uc: Raw Uncompensated
- mag_1_c: Professional compensation

mag_1_c will be our reference

Plot scalar magnetometers during T-L manuevers

Code 
use_mags = [:mag_1_c, :mag_2_uc, :mag_3_uc, :mag_4_uc, :mag_5_uc];
p = plot_mag(xyz; ind=TL_ind, use_mags = use_mags);
plot(p; single_pane_defs...);

Tail Stinger:
- mag_1_c Reference

Cabin:
- mag_2_uc Dead zones
- mag_3_uc
- mag_4_uc
- mag_5_uc

Plot scalar magnetometers during T-L manuevers

Code 
use_mags = [:mag_1_c, :mag_1_uc, :mag_3_uc, :mag_4_uc, :mag_5_uc];
p = plot_mag(xyz; ind=TL_ind, use_mags = use_mags);
plot(p; single_pane_defs...);

Tail Stinger:
- mag_1_c Reference

Cabin:
- mag_2_uc Dead zones
- mag_3_uc
- mag_4_uc
- mag_5_uc

Plot scalar mags during T-L manuevers (detrend)

Code 
use_mags = [:mag_1_c, :mag_3_uc, :mag_4_uc, :mag_5_uc];

p = plot_mag(xyz; detrend_data=true, ind=TL_ind, use_mags = use_mags);
plot(p; single_pane_defs...);

Wierd slope removal Mean removed from all

Tail Stinger:
- mag_1_c Reference

Cabin:
- mag_2_uc Dead zones
- mag_3_uc
- mag_4_uc
- mag_5_uc

Plot vector magnetometers during T-L manuevers

Code 
p = plot_mag(xyz; detrend_data=false, ind=TL_ind, use_mags = [:flux_d]);
plot(p; single_pane_defs...);

Create the Tolles-Lawson model

Compute \(c_i\)

Code 
λ       = 0.025;   # ridge parameter
use_vec = :flux_d; # selected vector (flux) magnetometer 
flux    = getfield(xyz,use_vec); # load Flux D data
TL_d_4  = create_TL_coef(flux,xyz.mag_4_uc,TL_ind;λ=λ);
Code 
TL_d_3  = create_TL_coef(flux,xyz.mag_3_uc,TL_ind;λ=λ); # create Tolles-Lawson
TL_d_5  = create_TL_coef(flux,xyz.mag_5_uc,TL_ind;λ=λ); # create Tolles-Lawson

Apply compensation to data

Code 
A = create_TL_A(flux,TL_ind);      # Tolles-Lawson "A" matrix for Flux D
mag_1_sgl = xyz.mag_1_c[TL_ind];   # professionally compensated tail stinger, Mag 1
mag_4_uc  = xyz.mag_4_uc[TL_ind]; # uncompensated Mag 4
mag_4_c   = mag_4_uc - detrend(A*TL_d_4;mean_only=true); # compensated Mag 4
Code 
mag_3_uc  = xyz.mag_3_uc[TL_ind]; # uncompensated Mag 3
mag_3_c   = mag_3_uc - detrend(A*TL_d_3;mean_only=true); # compensated Mag 3

mag_5_uc  = xyz.mag_5_uc[TL_ind]; # uncompensated Mag 5
mag_5_c   = mag_5_uc - detrend(A*TL_d_5;mean_only=true); # compensated Mag 5

Look at compensation results

Applied to the compensation data

Magnetometer 4 300 nT/division

Code 
p = plot(
     traj_flt.tt[TL_ind],
     mag_4_uc,
     xlabel="Time [seconds]",
     ylabel="Magnetic intensity [nT]",
     legend=true,
     label="Uncomp Mag 4",
     linecolor=:green
);
plot!(
     traj_flt.tt[TL_ind],
     mag_4_c,
     label="Comp Mag 4",
     linecolor=:black
)
plot(p; double_pane_defs...)

Magnetometer 5 100 nT/division

Code 
p = plot(
     traj_flt.tt[TL_ind],
     mag_5_uc,
     xlabel="Time [seconds]",
     ylabel="Magnetic intensity [nT]",
     legend=true,
     label="Uncomp Mag 5",
     linecolor=:green
);
plot!(
     traj_flt.tt[TL_ind],
     mag_5_c,
     label="Comp Mag 5",
     linecolor=:black
)
plot(p; double_pane_defs...)

Apply compensation to flight data

Dataframe df_nav has all the navigation flight lines

Code 
map_name   = :Eastern_395 # specify map, full list of maps in df_map
df_options = df_nav[(df_nav.flight   .== flight  ) .& # full list of navigation-capable flight lines is in df_nav
                    (df_nav.map_name .== map_name),:] # flight line options that are valid for the selected flight & map

2 rows × 8 columns

flight line t_start t_end full_line map_name map_type traj_alt
Symbol Float64 Float64 Float64 Bool Symbol Symbol Int64
1 Flt1006 1006.08 55770.0 56609.0 1 Eastern_395 HAE 397
2 Flt1006 1006.09 56965.0 57480.0 0 Eastern_395 HAE 574

Select line 1006.08 and get its indices:

Code 
line = df_options.line[1] # select flight line (row) from df_options
ind  = get_ind(xyz,line,df_nav); # get indices

Apply T-L compensation to selected flight line

Code 
A = create_TL_A(flux,ind);      # Tolles-Lawson "A" matrix for Flux D
mag_1_sgl = xyz.mag_1_c[ind];   # professionally compensated tail stinger, Mag 1
mag_4_uc  = xyz.mag_4_uc[ind]; # uncompensated Mag 4
mag_4_c   = mag_4_uc - detrend(A*TL_d_4;mean_only=true); # compensated Mag 4
Code 
mag_3_uc  = xyz.mag_3_uc[ind]; # uncompensated Mag 3
mag_3_c   = mag_3_uc - detrend(A*TL_d_3;mean_only=true); # compensated Mag 3

mag_5_uc  = xyz.mag_5_uc[ind]; # uncompensated Mag 5
mag_5_c   = mag_5_uc - detrend(A*TL_d_5;mean_only=true); # compensated Mag 5

Plot compensation results on flight data

Magnetometer 4 300 nT/division

Code 
p = plot(
     traj_flt.tt[ind],
     mag_4_uc,
     xlabel="Time [seconds]",
     ylabel="Magetic intensity [nT]",
     legend=true,
     label="Uncomp Mag 4",
     linecolor=:green
);
plot!(
     traj_flt.tt[ind],
     mag_4_c,
     label="Comp Mag 4",
     linecolor=:black
)
plot!(
     traj_flt.tt[ind],
     mag_1_sgl,
     label="Comp tail Stinger",
     linecolor=:red
)
plot!(p; double_pane_defs...)

Magnetometer 5 100 nT/division

Code 
p = plot(
     traj_flt.tt[ind],
     mag_5_uc,
     xlabel="Time [seconds]",
     ylabel="Magetic intensity [nT]",
     legend=true,
     label="Uncomp Mag 5",
     linecolor=:green
);
plot!(
     traj_flt.tt[ind],
     mag_5_c,
     label="Comp Mag 5",
     linecolor=:black
)
plot!(
     traj_flt.tt[ind],
     mag_1_sgl,
     label="Comp tail Stinger",
     linecolor=:red
)
plot!(p; double_pane_defs...)

Compare to professional calibration

Magnetometer 4

Code 
p = plot(
     traj_flt.tt[ind],
     detrend(mag_4_c-mag_1_sgl;mean_only=true),
     xlabel="Time [seconds]",
     ylabel="Magnetic intensity [nT]",
     legend=true,
     linecolor=:black,
     label="Comp 4 - Comp Stinger"
)
plot!(
     traj_flt.tt[ind],
     detrend(mag_4_uc-mag_1_sgl;mean_only=true),
     linecolor=:green,
     label="Uncomp 4 - Comp Stinger"
)
plot!(p; double_pane_defs...)

Magnetometer 5

Code 
p = plot(
     traj_flt.tt[ind],
     detrend(mag_5_c-mag_1_sgl;mean_only=true),
     xlabel="Time [seconds]",
     ylabel="Magnetic intensity [nT]",
     legend=true,
     linecolor=:black,
     label="Comp 5 - Comp Stinger"
)
plot!(
     traj_flt.tt[ind],
     detrend(mag_5_uc-mag_1_sgl;mean_only=true),
     linecolor=:green,
     label="Uncomp 5 - Comp Stinger"
)
plot!(p; double_pane_defs...)

Compare to professional calibration

Magnetometer 4

Code 
p = plot(
     traj_flt.tt[ind],
     detrend(mag_4_c;mean_only=true),
     xlabel="Time [seconds]",
     ylabel="Magnetic intensity [nT]",
     legend=true,
     linecolor=:black,
     label="Comp 4"
)
plot!(
     traj_flt.tt[ind],
     detrend(mag_1_sgl;mean_only=true),
     linecolor=:green,
     label="Comp Stinger"
)
plot!(p; double_pane_defs...)

Magnetometer 5

Code 
p = plot(
     traj_flt.tt[ind],
     detrend(mag_5_c;mean_only=true),
     xlabel="Time [seconds]",
     ylabel="Magnetic intensity [nT]",
     legend=true,
     linecolor=:black,
     label="Comp 5"
)
plot!(
     traj_flt.tt[ind],
     detrend(mag_1_sgl;mean_only=true),
     linecolor=:green,
     label="Comp Stinger"
)
plot!(p; double_pane_defs...)

Magnetic Navigation filter

  • Uses an Inertial Navigation System (INS)
  • Magnetic Navigation is a map-matching process
    • sequential estimation
    • single measurement value compared to map
  • Navigator provides error correction to the drifting INS solution
  • Kalman filter variant
    • Extended Kalman filter

Navigator overview - Extended Kalman Filter

State vector

\[ \vec{x}= \begin{bmatrix} \smash[b]{\underbrace{\begin{matrix} \delta \vec{p} & \delta \vec{v} & \delta \vec{\epsilon} & \vec{b}_a & \vec{b}_g\end{matrix}}_{\text{Pinson 15}}} & \smash[b]{\underbrace{\begin{matrix}\delta h_a & \delta a\end{matrix}}_{\text{Baro}}} & S_\text{fogm} & S_\text{bias} \end{bmatrix} \]

Measurement processor

\[ z = h(\vec{x}) + v \] \[ h(\vec{x}) = |B_\mathrm{a}| + |B_\text{earth}| + {\color{gray}|B_\text{Plane}}| + S_\text{fogm} + S_\text{bias} \]

Where

  • \(|B_\mathrm{a}|\) comes from map interpolation
  • \(|B_\text{earth}|\) World Magnetic Model
  • \(|B_\text{Plane}|\) aircraft disturbance field - not included here with SGL calibration
  • \(S_\text{fogm}\) scalar state estimates of space-weather
  • \(S_\text{bias}\) offset bias between map and measurement

Required data sources

  • Inertial Navigation System (INS)
    • Angle rates, \(\Delta\theta\)
    • Accelerations/specific forces, \(\Delta\vec{v}\)
  • Barometer
    • Precise but not accurate
    • Stablize the altitude
  • Magnetometers
    • Scalar - primary sensor
    • Vector - for compensation
  • Magnetic Map
    • Core field model e.g. WMM or IGRF
    • Magnetic anomaly map

Kalman filter review

Discrete time dynamics at time index \(k+1\) the state vector \(\vec{x}_{k+1}\) is \[ \vec{x}_{k+1} = {\Phi}_k \vec{x}_k + {B}_k \vec{u}_k + \vec{w}_k \]

  • \(\Phi_k\) is the state transition matrix
  • \(B_k\) is the input or control matrix
    • we are not supplying control, so \(B=0\)
  • \(\vec{w}\sim \mathcal{N}(0,{Q})\) is Gaussian white noise process with covariance matrix \({Q}\)

A measurement \(\vec{z}\) is \[ \vec{z}_k = {H}_k \vec{x}_k + \vec{v}_k \]

  • \({H}\) is connection between state \(\vec{x}\) and measurement \(\vec{z}\)

  • \(\vec{v}\sim\mathcal{N}(0,{R})\) is the noise process of the measurement with covariance \({R}\)

  • (Brown and Hwang 2012)

The state \(\vec{x}_{k}\) has a mean \(\hat{\vec{x}}_{k}\) and covariance \({P}_{k}\) which propagates forward in time (with no other information) like: \[ \begin{aligned} \hat{\vec{x}}_{k+1}^- & = {\Phi}_k \hat{\vec{x}}_{k} + \cancelto{0}{{B}\vec{u}_k} \\ {P}_{k+1}^- & = {\Phi}_k {P}_{k} {\Phi}_k^T + {Q}_k \end{aligned} \] When a measurement \(\vec{z}\) is made, we can update the propagated state vector \[ \begin{aligned} \hat{\vec{x}}_{k} &= \hat{\vec{x}}_{k}^- + {K}_k (\vec{z}_k - {H}_k \hat{\vec{x}}_{k}^-)\\ {P}_k &= ({I} -{K}_k {H}_k ) {P}_{k}^- \\ {K}_k &= {P}_{k}^- {H}_k^T( {H}_k {P}_{k}^- {H}_k^T + {R}_k )^{-1} \end{aligned} \]

Kalman filter flow diagram

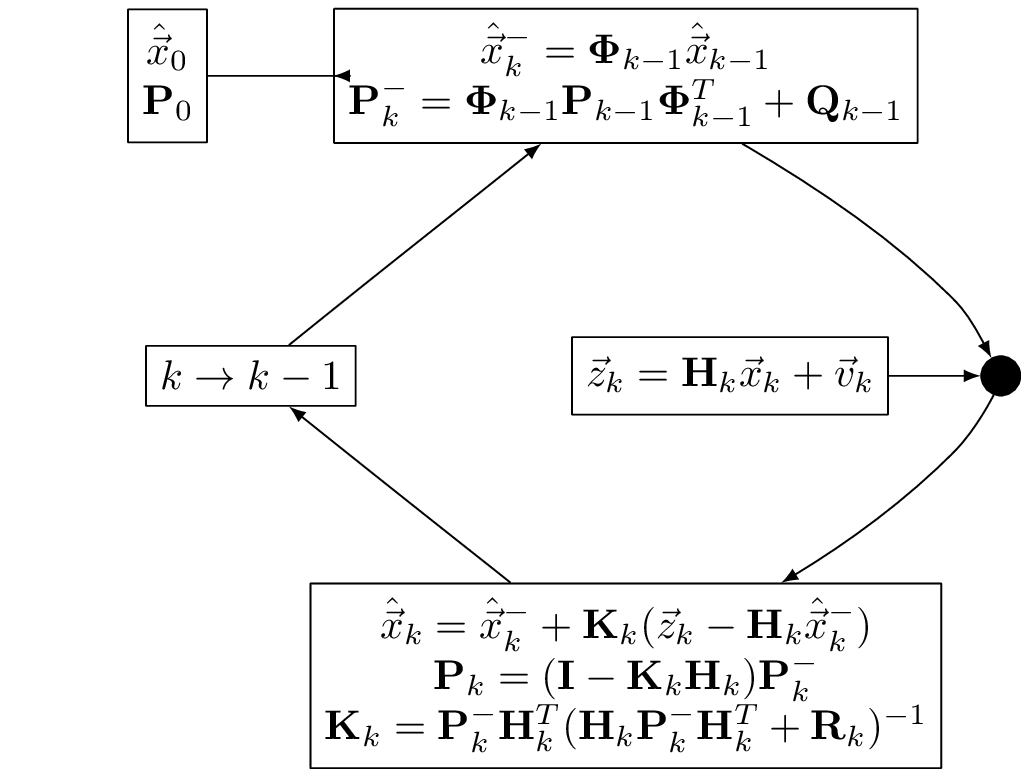
Linearization for navigation

The map-matching measurement processor is non-linear. Two primary approaches have been used for MagNav:

Linearization of Kalman filter

Generalize the state dynamics and measurement \[ \begin{aligned} \dvec{x} & = \vec{f}(\vec{x}, \vec{u}_d, t) + \vec{u}(t) \\ \vec{z} & = \vec{h}(\vec{x}, t) + \vec{v}(t) \end{aligned} \]

  • \(\vec{f}(\vec{x}, \vec{u}_d, t)\) and \(\vec{h}(\vec{x}, t)\) are known functions
  • \(\vec{u}_d\) deterministic forcing function (e.g. gravity)
  • \(\vec{u}\) and \(\vec{v}\) are uncorrelated white noise processes

Write the state \(\vec{x}\) in terms of some \(\vec{x}^*(t)\) and a deviation from it \(\Delta\vec{x}(t)\) \[ \vec{x}(t) = \vec{x}^*(t) + \Delta\vec{x}(t) \]

Linearization of Kalman filter

\[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & = \vec{f}(\vec{x}^* + \Delta\vec{x}, \vec{u}_d, t) + \vec{u}(t) \\ \vec{z} & = \vec{h}(\vec{x}^* +\Delta\vec{x}, t) + \vec{v}(t) \end{aligned} \]

\(\Delta\vec{x}\) is small and use Taylor series (so many Taylor series) \[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & \approx \vec{f}(\vec{x}^*, \vec{u}_d, t) + \left[ \frac{\partial \vec{f}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{u}(t) \\ \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \] If \(\vec{x}^*\) is just a single known trajectory, then this is just the Linearized Kalman filter.

If \(\vec{x}^*\) is our trajectory estimate, then this is the Extended Kalman filter.

Equivalent linearized represenation

\[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & \approx \vec{f}(\vec{x}^*, \vec{u}_d, t) + \left[ \frac{\partial \vec{f}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{u}(t) \\ \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \] Becomes \[ \begin{aligned} \dvec{x}^* + \Delta\dvec{x} & \approx \vec{f}(\vec{x}^*, \vec{u}_d, t) + \mat{F} \cdot \Delta\vec{x} + \vec{u}(t) \\ \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \mat{H} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \] with \[ \mat{F} = \left[ \frac{\partial \vec{f}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*},\ \mat{H} = \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \]

Extended Kalman Filter (EKF)

Write the linearized measurement as \[ \vec{z} - \vec{h}(\vec{x}^*) = \mat{H} \Delta \vec{x} + \vec{v} \] The incremental estimate update at time \(t_k\) is \[ \Delta\hat{\vec{x}}_k = \Delta\hat{\vec{x}}_k^- + \mat{K}_k \left[ \vec{z}_k - \vec{h}(\vec{x}^*_k) - \mat{H}_k \Delta\hat{\vec{x}}_k^- \right] \] Write the estimate of what the measurement should be \[ \hat{\vec{z}}^-_k = \vec{h}(\vec{x}^*_k) + \mat{H}_k \Delta\hat{\vec{x}}_k^- \] And then \[ \underbrace{\vec{x}^*_k + \Delta\hat{\vec{x}}_k}_{\textstyle\hat{\vec{x}}_k} = \underbrace{\vec{x}^*_k + \Delta\hat{\vec{x}}_k^-}_{\textstyle\hat{\vec{x}}_k^-} + \mat{K}_k \left[ \vec{z}_k - \hat{\vec{z}}^-_k \right] \]

EKF data flow

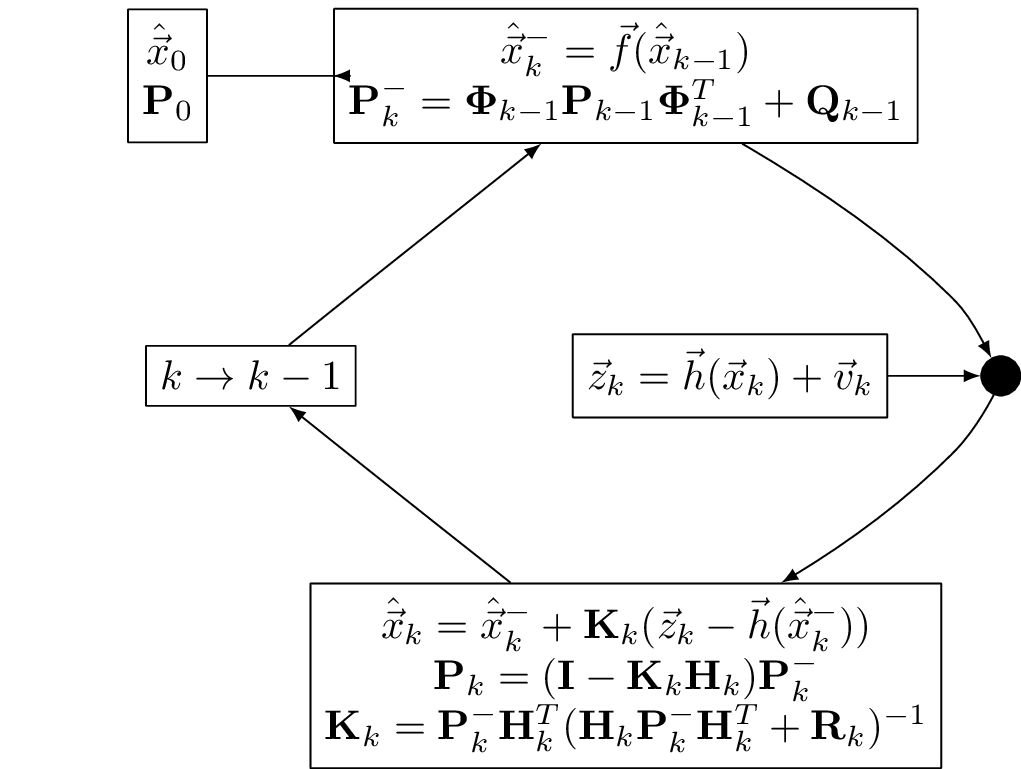
Pinson-9 model for inertial navigation

(Titterton and Weston 2004), (Raquet 2021)

Pinson 9-state model for INS is: \[ \vec{x} = \begin{bmatrix} \delta x_n \\ \delta x_e \\ \delta x_d \\ \delta v_n \\ \delta v_e \\ \delta v_d \\ \delta\epsilon_n \\ \delta\epsilon_e \\ \delta\epsilon_d \\ \end{bmatrix} = \begin{bmatrix} \delta\vec{x} \\ \delta\vec{v} \\ \delta\vec{\epsilon} \\ \end{bmatrix} \]

Where:

  • \(\delta\vec{x}\) are the NED position error states
  • \(\delta\vec{v}\) are the NED velocity error states
  • \(\delta\vec{\epsilon}\) are the angle atittude errors

and \[ \dvec{x} = \mat{F} \vec{x} \]

Pinson-9 model propagation

\[ \begin{bmatrix} \delta\dvec{x} \\ \delta\dvec{v} \\ \delta\dvec{\epsilon} \end{bmatrix} = \begin{bmatrix} F_{xx} & F_{xv} & F_{x\epsilon} \\ F_{vx} & F_{vv} & F_{v\epsilon} \\ F_{\epsilon x} & F_{\epsilon v} & F_{\epsilon \epsilon} \\ \end{bmatrix} \begin{bmatrix} \delta \vec{x} \\ \delta \vec{v} \\ \delta \vec{\epsilon} \\ \end{bmatrix} \] We are working in geodetic coordinates so the elements of \(\mat{F}\) depend upon Earth specifc parameters to account for Coriolis force.

Pinson-9 model propagation definitions

Variable Description Value/Units
\(\phi\) latitude radian
\(v_n\) north velocity meter/second
\(v_e\) east velocity meter/second
\(v_d\) down velocity meter/second
\(f_n\) north specific force meter/second/second
\(f_e\) east specific force meter/second/second
\(f_d\) down specific force meter/second/second
\(R_\earth\) Earth radius 635300 meter
\(\Omega_\earth\) Earth rotation rate 7.2921151467e-5/second

Components of \(\mat{F}\), \(F_x\) row

\[ F_{xx} = \begin{bmatrix} 0 & 0 & -\frac{v_n}{R_\earth^2}\\ \frac{v_e \tan \phi}{R_\earth\cos \phi} & 0 & \frac{v_e}{R_\earth^2 \cos\phi} \\ 0 & 0 & 0 \\ \end{bmatrix} \]

\[ F_{xv} = \begin{bmatrix} \frac{1}{R_\earth} & 0 & 0\\ 0 & \frac{1}{R_\earth\cos\phi} & 0 \\ 0 & 0 & -1 \\ \end{bmatrix} \]

\[ F_{x\epsilon} = \mat{0}_{3\times 3} \]

\(F_v\) row of \(\mat{F}\)

\[ F_{vx} = \begin{bmatrix} v_e \left( 2\Omega_\earth\cos\phi + \frac{v_e}{R_\earth\cos^2\phi} \right) & 0 & \frac{v_e^2\tan\phi - v_n v_d}{R_\earth^2}\\ 2\Omega_\earth \left(v_n \cos\phi - v_d \sin\phi\right) + \frac{v_n v_e}{R_\earth \cos^2\phi} & 0 & \frac{-v_e (v_n\tan\phi +v_d)}{R_\earth^2}\\ 2\Omega_\earth v_e \sin \phi & 0 & \frac{v_n^2 + v_e^2}{R_\earth} \\ \end{bmatrix} \]

\[ F_{vv} = \begin{bmatrix} \frac{v_d}{R_\earth} & -2 \left( \Omega_\earth \sin\phi + \frac{v_e\tan\phi}{R_\earth} \right) & \frac{v_n}{R_\earth} \\ 2\Omega_\earth\sin\phi + \frac{v_e\tan\phi}{R_\earth} & \frac{v_n\tan\phi+v_d}{R_\earth} & 2\Omega_\earth \cos\phi + \frac{v_e}{R_\earth} \\ -\frac{2v_n}{R_\earth} & -2 \left( \Omega_\earth \cos\phi + \frac{v_e}{R_\earth} \right) & 0 \\ \end{bmatrix} \]

\[ F_{v\epsilon} = \begin{bmatrix} 0 & -f_d & f_e \\ f_d & 0 & -f_n \\ -f_e & f_n & 0 \end{bmatrix} \]

\(F_\epsilon\) row of \(\mat{F}\)

\[ F_{\epsilon x} = \begin{bmatrix} -\Omega_\earth \sin\phi & 0 & -\frac{v_e}{R_\earth} \\ 0 & 0 & \frac{v_n}{R_\earth^2} \\ -\Omega_\earth \cos\phi - \frac{v_e}{R_\earth \cos^2\phi} & 0 & \frac{v_e\tan\phi}{R_\earth^2} \end{bmatrix} \]

\[ F_{\epsilon v } = \begin{bmatrix} 0 & 1/R_\earth & 0 \\ -1/R_\earth & 0 & 0 \\ 0 & \frac{\tan\phi}{R_\earth} & 0 \\ \end{bmatrix} \]

\[ F_{\epsilon\epsilon} = \begin{bmatrix} 0 & -\Omega_\earth\sin\phi + \frac{v_e}{R_\earth\tan\phi} & v_n/R_\earth \\ \Omega_\earth\sin\phi + \frac{v_e\tan\phi}{R_\earth} & 0 & \Omega_\earth\cos\phi + v_e/R_\earth \\ -v_n/R_\earth & -\Omega\cos\phi -v_e/R_\earth & 0 \\ \end{bmatrix} \]

Pinson-15 state model

  • Extends the 9-state model to include
  • accelerometer \(\vec{b_a}\) and gyro \(\vec{b_g}\) biases
  • using First Order Gauss Markov model (FOGM)

\[ \vec{x} = \begin{bmatrix} \delta x_n \\ \delta x_e \\ \delta x_d \\ \delta v_n \\ \delta v_e \\ \delta v_d \\ \delta\epsilon_n \\ \delta\epsilon_e \\ \delta\epsilon_d \\ b_{a_x} \\ b_{a_y} \\ b_{a_z} \\ b_{g_x} \\ b_{g_y} \\ b_{g_z} \\ \end{bmatrix} = \begin{bmatrix} \delta\vec{x} \\ \delta\vec{v} \\ \delta\vec{\epsilon} \\ \vec{b_a}\\ \vec{b_g}\\ \end{bmatrix} \]

Propagation for 15-state Pinson model

\[ \begin{bmatrix} \delta\dvec{x} \\ \delta\dvec{v} \\ \delta\dvec{\epsilon} \\ \dvec{b_a}\\ \dvec{b_g}\\ \end{bmatrix} = \begin{bmatrix} F_{xx} & F_{xv} & 0 & 0 & 0\\ F_{vx} & F_{vv} & F_{v\epsilon} & \mat{C}_b^n & 0 \\ F_{\epsilon x} & F_{\epsilon v} & F_{\epsilon \epsilon} & 0 & -\mat{C}_b^n \\ 0 & 0 & 0 & F_{aa} & 0 \\ 0 & 0 & 0 & 0 & F_{gg} \\ \end{bmatrix} \begin{bmatrix} \delta \vec{x} \\ \delta \vec{v} \\ \delta \vec{\epsilon} \\ \vec{b}_a\\ \vec{b}_g\\ \end{bmatrix} \]

\[ F_{aa} = \begin{bmatrix} -1/\tau_a & 0 & 0 \\ 0 & -1/\tau_a & 0 \\ 0 & 0 & -1/\tau_a\\ \end{bmatrix},\ F_{gg} = \begin{bmatrix} -1/\tau_g & 0 & 0 \\ 0 & -1/\tau_g & 0 \\ 0 & 0 & -1/\tau_g\\ \end{bmatrix} \] and \(\mat{C}_b^n\) is the direction cosine matrix that rotates from body to NED frame.

MagNav additions to Pinson-15

  • Add a barometer altimeter to constrain Altitude
    • \(\delta h_a\) is the altitude error correction to the INS
    • \(\delta a\) is the vertical acceleration error (we already have \(\delta v_n\) in Pinson-9)
  • Add a state \(S\) to model external time-correlated magnetic field variations
    • space weather
    • effects must be out-side of navigation frequency band

Results in an 18-component state vector \[ \begin{bmatrix} \delta \vec{x} & \delta \vec{v} & \delta \vec{\epsilon} & \vec{b}_a & \vec{b}_g & \delta h_a & \delta a & S \end{bmatrix} \]

Updates to \(\mat{F}\) matrix

\[ \begin{bmatrix} \delta\dvec{x} \\ \delta\dvec{v} \\ \delta\dvec{\epsilon} \\ \dvec{b}_a\\ \dvec{b}_g\\ \dot{h_a}\\ \dot{\delta_a}\\ \dot{S} \end{bmatrix} = \begin{bmatrix} F_{xx} & F_{xv} & 0 & 0 & 0 & F_{xb} & 0 \\ F_{vx} & F_{vv} & F_{v\epsilon} & \mat{C}_b^n & 0 & F_{vb} & 0 \\ F_{\epsilon x} & F_{\epsilon v} & F_{\epsilon \epsilon} & 0 & -\mat{C}_b^n & 0 & 0 \\ 0 & 0 & 0 & F_{aa} & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & F_{gg} &0 & 0 \\ F_{bp} & 0 & 0 & 0 & 0 & F_{bb} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & F_{ss} \\ \end{bmatrix} \begin{bmatrix} \delta \vec{x} \\ \delta \vec{v} \\ \delta \vec{\epsilon} \\ \vec{b}_a\\ \vec{b}_g\\ \delta h_a \\ \delta a \\ S \end{bmatrix} \]

Updated \(\mat{F}\) components

Barometer aiding: \[ \mat{F}_{xb} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ k_1 & 0 \end{bmatrix},\ \mat{F}_{vb} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ -k_2 & 1 \\ \end{bmatrix} \]

\[ \mat{F}_{bx} = \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & k_3 \\ \end{bmatrix},\ \mat{F}_{bb} = \begin{bmatrix} -\frac{1}{\tau_b} & 0 \\ -k_3 & 0 \\ \end{bmatrix} \]

The space weather, diurnal bias is given by: \[ \mat{F}_{ss} = \frac{1}{\tau_s} \]

MagNav measurement processor

The scalar sensor measures: \[ |\vec{B}_\text{total}| = |\vec{B}_\ext + \vec{B}_\text{\faPlane} | \] and \[ \vec{B}_\ext = \vec{B}_\earth+ \vec{B}_\text{anomaly} + \vec{B}_\text{disturbance} \]

  • We added a state \(S\) into the MagNav model to account for \(\vec{B}_\text{disturbance}\).
  • \(\vec{B}_\earth\) from IGRF or WMM
    • Both IGRF and WMM are functions of lat, long, altitude and time
    • WMM has \(28.8^\circ\) or 3200 km at surface resolution
    • Secular variaton \(\approx 100 \text{nT}/\text{year} = 0.27 \text{nT}/\text{day}\)

MagNav Measurement Processor \(H\) matrix

\[ \begin{aligned} \vec{z} & \approx \vec{h}(\vec{x}^*, t) + \mat{H} \cdot \Delta\vec{x} + \vec{v}(t) \end{aligned} \]

\[ \mat{H} = \left[ \frac{\partial \vec{h}}{\partial \vec{x}}\right]_{\vec{x}=\vec{x}^*} \]

\[ \mat{H}(\vec{x}^*) = \begin{bmatrix} \frac{\partial h(\vec{x}^*)}{\partial x_n} \\ \frac{\partial h(\vec{x}^*)}{\partial x_e} \\ \frac{\partial h(\vec{x}^*)}{\partial x_d} \\ \mat{0}_{1x15} \end{bmatrix} \leftarrow\text{This is the gradient of the map} \] Both the map and 3D gradient of the map are needed in order to make a measurement and incorporate it.

Filter initialization

  • Assume known starting value for position and attitude from GPS-aided system
    • Tolles-Lawson coefficients are needed
  • Works well for EKF - provides excellent starting point for state
    • State starting point initializes map error state \(S\)
  • Particle filter initialization
    • Randomly draw ensemble of \(N\) particles from my anticpated distribution
    • This includes a position \(\vec{x}\) and map bias \(S\) hypothesis

MagNav.jl

MagNav.jl software does not have it’s own INS mechanization code

  • relies on an INS to provide the solution around which the EKF is linearized
  • fine provided that the solution remains in the linear regime
    • too much INS drift will break this assumption
  • Two-dimensional navigation
    • aircraft is assumed at constant altitude

Data for Navigation

  • traj: GPS truth trajectory
  • ins: pure inertial trajectory solution
  • map: magnetic anomaly maps at flight altitude
  • mag: magnetic measurement data from aircraft
    • Use Tolles-Lawson calibration computed earlier
    • ground station for diurnal and space weather

Find flight path for navigation

Code 
map_name   = :Eastern_395 # specify map, full list of maps in df_map
df_options = df_nav[(df_nav.flight   .== flight  ) .& # full list of navigation-capable flight lines is in df_nav
                    (df_nav.map_name .== map_name),:] # flight line options that are valid for the selected flight & map

2 rows × 8 columns

flight line t_start t_end full_line map_name map_type traj_alt
Symbol Float64 Float64 Float64 Bool Symbol Symbol Int64
1 Flt1006 1006.08 55770.0 56609.0 1 Eastern_395 HAE 397
2 Flt1006 1006.09 56965.0 57480.0 0 Eastern_395 HAE 574
Code 
line = df_options.line[1] # select flight line (row) from df_options
ind  = get_ind(xyz,line,df_nav); # get indices

Plot navigation trajectory (GPS)

Entire map

Code 
p3 = plot_map(mapS;legend=false); # plot map 
plot_path!(p3,traj_flt,ind;path_color=:black);

Zoom on selected flight line

Code 
p3 = plot_map(mapS;legend=false); # plot map background
plot_path!(p3,traj_flt,ind;path_color=:black,show_plot=false,zoom_plot=true); # plot gps
plot!(p3,legend=:topleft) # move legend as desired

Plot navigation trajectory (GPS and INS)

Entire map

Code 
p3 = plot_map(mapS;legend=false); # plot map 
plot_path!(p3,traj_flt,ind;path_color=:black);

Zoom on selected flight line

Code 
p3 = plot_map(mapS;legend=false); # plot map background
plot_path!(p3,traj_flt,ind;path_color=:black,show_plot=false,zoom_plot=true); # plot GPS
plot_path!(p3,ins_flt,ind;path_color=:red,show_plot=false,zoom_plot=true)
plot!(p3,legend=:topleft) # move legend as desired

GPS track
INS only

Notice overall shift between tracks

Set up data for navigation

Code 
# get trajectory (gps) struct
traj = get_traj(xyz,ind); 

# get INS struct, force ("zero") the lat/lon to match `traj` for 1 data point
ins  = get_ins(xyz,ind;N_zero_ll=1);

Uncorrected GPS and INS tracks

Code 
p3 = plot_map(mapS;legend=false); # plot map background
plot_path!(p3,traj_flt,ind;path_color=:black,show_plot=false,zoom_plot=true); # plot GPS
plot_path!(p3,ins_flt,ind;path_color=:red,show_plot=false,zoom_plot=true)
plot!(p3,legend=:topleft) # move legend as desired
plot(p3; double_pane_defs...)

\(\rightarrow\)

Shifted GPS and INS tracks

Code 
p3 = plot_map(mapS;legend=false); # plot map background
plot_path!(p3,traj;path_color=:black,show_plot=false,zoom_plot=true); # plot GPS
plot_path!(p3,ins;path_color=:red,show_plot=false,zoom_plot=true)
plot!(p3,legend=:topleft) # move legend as desired
plot(p3; double_pane_defs...)

Upward continue and prepare map

Code 
# load map data
mapS_orig = get_map(map_name,df_map); 

# upward continue map to mean altitude of traj
mapS = upward_fft(mapS_orig,mean(traj.alt));

Original map at 395 meter altitude

Code 
p3 = plot_map(mapS;legend=false)
plot(p3; double_pane_defs...)

Upward continued map at 398 m altitude

Code 
p3 = plot_map(mapS_orig;legend=false)
plot(p3; double_pane_defs...)

Compare map value with magnetometer values

Code 
# create interpolation function
itp_mapS = map_interpolate(mapS); 

# interpolate along traj and add in core & diurnal
map_val  = itp_mapS.(traj.lon,traj.lat) + (xyz.igrf + xyz.diurnal)[ind];
Code 
p = plot(
    traj.tt,
    map_val,
    xlabel="Time [seconds]",
    ylabel="Magnetic magnitude [nT]",
    legend=true,
    label="Map value");
plot!(
    traj.tt,
    mag_1_sgl,
    label="Stinger value");
plot!(
    traj.tt,
    mag_4_c,
    label="Comp Mag 4")
plot(p; double_pane_defs...)

Code 
p = plot(
    traj.tt,
    map_val .- mag_1_sgl,
    xlabel="Time [seconds]",
    ylabel="Magnetic residual [nT]",
    legend=true,
    label="Map - stinger");
plot!(
    traj.tt,
    map_val .- mag_4_c,
    legend=true,
    label="Map - Comp Mag 4")
plot(p; double_pane_defs...)

Create EKF filter model

FOGM filter tuning parameters

Code 
plot_autocor(mag_4_c-map_val)

EKF filter generation

Code 
(P0,Qd,R) = create_model(traj.dt,traj.lat[1];
                         init_pos_sigma = 0.1,
                         init_alt_sigma = 1.0,
                         init_vel_sigma = 1.0,
                         meas_var       = 134^2, # increase for bad mag
                         fogm_sigma     = 134,
                         fogm_tau       = 10.0);

Run the filter

Code 
mag_use = mag_4_c; # specify using Mag 4 for navigation
mag_use .+= map_val[1]-mag_use[1]; # remove initial DC offset
(crlb_out_4,ins_out_4,filt_out_4) = run_filt(traj,ins,mag_use,itp_mapS,:ekf;P0,Qd,R,core=true); # run the filter

Mag 4 DRMS Error = 149.2 meter

Mag 5 DRMS Error = 82.5 meter

INS DRMS Error = 137.5 meter

North position error

Code 
tt_min = (traj.tt .- traj.tt[1])./60;
p=error_plot(tt_min,filt_out_4.n_err,filt_out_4.n_std, color=:blue, label="Mag 4, North error",xlabel="Time [minutes]", ylabel="North Error [meters]")
error_plot(p,tt_min,filt_out_5.n_err,filt_out_5.n_std, color=:green,label="Mag 5, North error",xlabel="Time [minutes]", ylabel="North Error [meters]")
plot(p; double_pane_defs...)

East position error

Code 
p=error_plot(tt_min,filt_out_4.e_err,filt_out_4.e_std, color=:blue, label="Mag 4, East error",xlabel="Time [minutes]", ylabel="East Error [meters]")
error_plot(p,tt_min,filt_out_5.e_err,filt_out_5.e_std, color=:green, label="Mag 5, East error",xlabel="Time [minutes]", ylabel="East Error [meters]")
plot(p; double_pane_defs...)

Inertial only solution

Code 
p = error_plot(
    tt_min,
    ins_out_4.n_err,
    ins_out_4.n_std; label="North error",xlabel="Time [minutes]", ylabel="North Error [meters]")
plot(p; double_pane_defs...)

Code 
p = error_plot(
    tt_min,
    ins_out_4.e_err,
    ins_out_4.e_std, label="East error",xlabel="Time [minutes]", ylabel="East Error [meters]")
plot(p; double_pane_defs...)

Plot filter results

Conclusion

Conclusion

You should be familiar with Magnetic Navigation

  • Maps
  • Calibration
  • Navigation

You should know how to use MagNav.jl to explore navigation

  • software
  • data

Questions?

ANT Center

Contact information

Contact information

Aaron Nielsen
Air Force Institute of Technology (AFIT) https://www.afit.edu
Autonomy and Navigation Technology Center (ANT Center) https://www.afit.edu/ANT/

References

Backups

Maps

Scalar magnetic potentials

Scalar Magnetic Potential \(\Phi_M\)

  • If \(\vec{J} = 0\), then \(\nabla \times \vec{H} = 0\)
  • \(\vec{H}(\vec{r}) = -\nabla \Phi_M(\vec{r})\)
  • and since \(\nabla \cdot \vec{B} = 0 \rightarrow \nabla^2 \Phi_M(\vec{r}) = 0\)
  • LaPlacian equation: \(\nabla^2 \Phi_M(\vec{r}) = 0\)
  • Solutions are often referred to as harmonic (sins and cosins)
  • This situation holds for many airborne problems

(Blakely 1995)

Scalar Potential Theory

A procedure to transform magnetic scalar potential \(\Phi_M\) in free space.

From Laplacian we can write (Green’s third identity) \[ \Phi_M(\vec{r}) = \frac{1}{4\pi} \int_S \left( \frac{1}{r} \frac{\partial \Phi_M}{\partial n} - \Phi_M \frac{\partial}{\partial n} \frac{1}{r} \right) dS \]

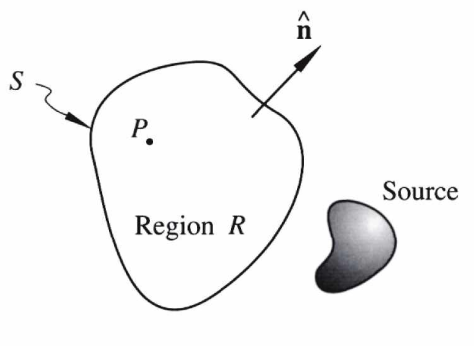
  • No sources in region \(R\)
  • Know \(\Phi_M\) on the surface \(S\) that bounds \(R\)
  • We can find \(\Phi_M\) anywhere in \(R\)
  • (Blakely 1995)

Hemispherical geometry - flat Earth model

  • Think of Earth’s surface as an infinite flat plane, all sources below
  • Measure the potential on a plane above the earth
  • Other side of hemisphere is \(\infty\) away and therefore zero potential
  • Potential anywhere inside can be computed

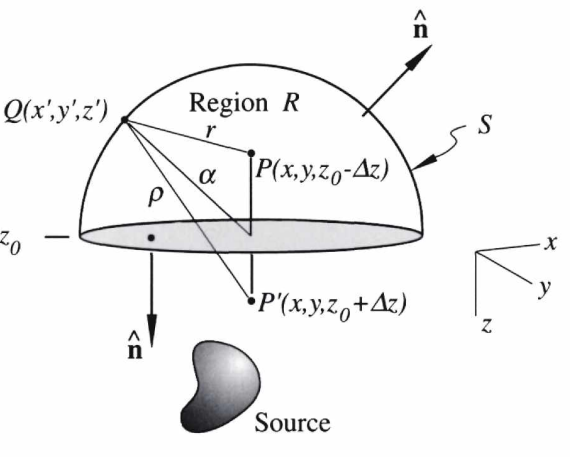
Fourier methods for potential theory

  • Goal: find the potential \(\Phi_M\) on a plane parallel to a known plane
  • Process: double integral over the surface of the known plane
  • Ends up looking like a 2-D Fourier transform over spatial coordinates
  • (Blakely 1995)

ION/IEEE PLANS MagNav Tutorial 2023

Bankey, Viki, Alejandro Cuevas, David Daniels, Carol A. Finn, Israel Hernandez, Patricia Hill, Robert Kucks, et al. 2002. “Digital Data Grids for the Magnetic Anomaly Map of North America.” U.S. Department of the Interior, U.S. Geological Survey; Online; US Geological Survey. https://doi.org/10.3133/ofr02414.
Blakely, Richard J. 1995. Potential Theory in Gravity and Magnetic Applications. Cambridge University Press.
Brown, Robert Grover, and Patrick Y C Hwang. 2012. Introduction to random signals and applied kalman filtering: with MATLAB exercises and solutions; 4th ed. New York, NY: Wiley.
Canciani, Aaron J. 2016. “Absolute Positioning Using the Earth’s Magnetic Field.” PhD thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/251.
———. 2021. “Magnetic Navigation on an f-16 Aircraft Using Online Calibration.” IEEE Trans. Aerospace and Electronic Systems. https://doi.org/10.1109/TAES.2021.3101567.
Chulliat, A.;W. Brown;P. Alken;C. Beggan;M. Nair;G. Cox;A. Woods;S. Macmillan;B. Meyer;M. Paniccia; 2020. “The US/UK World Magnetic Model for 2020-2025 : Technical Report.” National Centers for Environmental Information (U.S.);British Geological Survey. https://doi.org/10.25923/ytk1-yx35.
Clarke, Daniel J. 2021. “Real-Time Aerial Magnetic and Vision-Aided Navigation.” Master’s thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/4994/.
Gelb, Arthur et al. 1974. Applied Optimal Estimation. MIT press.
Gnadt, Albert R., Joeseph Belarge, Aaron Cancini, Lauren Conger, Joseph Curro, Alan Edelman, Peter Morales, Michael O’Keefe, Jonathan Taylor, and Chrstopher Rackaukas. 2020. “Signal Enhancement for Magnetic Navigation Challenge Problem,” July. https://doi.org/10.48550/ARXIV.2007.12158.
Gnadt, Albert R., Allan B. Wollaber, and Aaron P. Nielsen. 2022. “Derivation and Extensions of the Tolles-Lawson Model for Aeromagnetic Compensation.” arXiv. https://doi.org/10.48550/ARXIV.2212.09899.
Leliak, Paul. 1961. “Identification and Evaluation of Magnetic-Field Sources of Magnetic Airborne Detector Equipped Aircraft.” IRE Transactions on Aeronautical and Navigational Electronics ANE-8 (3): 95–105. https://doi.org/10.1109/TANE3.1961.4201799.
McNeil, Alexander J. 2022. “Magnetic Anomaly Absolute Positioning for Hypersonic Aircraft.” Master’s thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/5457.
Meyer, B., A. Chulliat, and R. Saltus. 2017. “Derivation and Error Analysis of the Earth Magnetic Anomaly Grid at 2 Arc Min Resolution Version 3 (EMAG2v3).” Geochemistry, Geophysics, Geosystems 18 (12): 4522–37. https://doi.org/10.1002/2017gc007280.
Mount, Lauren A. 2018. “Navigation Using Vector and Tensor Measurements of the Earth’s Magnetic Anomaly Field.” Master’s thesis, Air Force Institute of Technology. https://scholar.afit.edu/etd/1817/.
Raquet, John. 2021. “Pinson 15 Model.”
Roberts, Carter W., and Robert C. Jachens. 2000. “Preliminary Aeromagnetic Anomaly Map of California.” United States Geologic Survey. https://pubs.usgs.gov/of/1999/0440/.
Titterton, David, and John Weston. 2004. Strapdown Inertial Navigation Technology. Institution of Engineering; Technology. https://doi.org/dx.doi.org/10.1049/PBRA017E.
Tolles, W E, and J D Lawson. 1950. “Magnetic compensation of MAD equipped aircraft.” Airborne Instruments Lab. Inc., Mineola, NY, Rept, 201–1.
Tolles, W. E. 1954. Compensation of aircraft magnetic fields. 2692970, issued 1954.
———. 1955. Magnetic field compensation system. 2706801, issued 1955.